
【题目】如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:∠A=90°,∠ABD=60°,∠CBD=54°,AB=200 m,BC=300 m.请你计算出这片水田的面积.(参考数据:sin 54°≈0.809,cos 54°≈0.588,tan 54°≈1.376,![]() =1.732)
=1.732)

【答案】83180
【解析】作CM⊥BD于M,由含30°角的直角三角形的性质求出BD,由勾股定理求出AD,求出△ABD的面积,再由三角函数求出CM,求出△BCD的面积,然后根据S四边形ABCD=S△ABD+S△BCD列式计算即可得解.
∵∠A=90°,∠ABD=60°,
∴∠ADB=30°,
∴BD=2AB=400 m,
∴AD=![]() AB=200
AB=200![]() m,
m,
∴△ABD的面积=![]() ×200×200
×200×200![]() =20000
=20000![]() m2.
m2.
∵∠CMB=90°,∠CBD=54°,
∴CM=BC·sin 54°=300×0.809=242.7m.
∴△BCD的面积=![]() ×400×242.7=48540m2.
×400×242.7=48540m2.
∴这片水田的面积=20000![]() +48 540≈83180m2.
+48 540≈83180m2.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
(1)若∠A=50°,∠D=30°,求∠GEF的度数;
(2)若BD=CE,求证:FG=BF+CG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批A、B两种型号的节能防近视台灯,每台进价分别为200元、170元,近两周的销售情况如下:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 进价、售价均保持不变,利润
进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本
进货成本![]()
![]() 求A、B两种型号的台灯的销售单价;
求A、B两种型号的台灯的销售单价;
![]() 若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
![]() 在
在![]() 的条件下,能否求出该商场销售完这30台台灯所获得的最大利润
的条件下,能否求出该商场销售完这30台台灯所获得的最大利润![]() 若能,求出最大利润;若不能,请说明理由.
若能,求出最大利润;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-2x+1=0.
(1)若方程有两个实数根,求m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2-x1-x2=![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
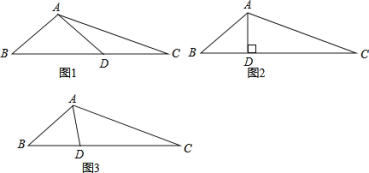
【题目】问题背景:在△ABC中,∠B=2∠C,点D为线段BC上一动点,当AD满足某种条件时,探讨在线段AB、BD、CD、AC四条线段中,某两条或某三条线段之间存在的数量关系.
例如:在图1中,当AB=AD时,可证得AB=DC,现在继续探索:
任务要求:
(1)当AD⊥BC时,如图2,求证:AB+BD=DC;
(2)当AD是∠BAC的角平分线时,判断AB、BD、AC的数量关系,并证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-3a经过A(-1,0),C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的表达式;
(2)已知点D(m,-m-1)在第四象限的抛物线上,求点D关于直线BC对称的点D′的坐标;
(3)在(2)的条件下,连接BD.问在x轴上是否存在点P,使∠PCB=∠CBD?若存在,请求出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线![]() 与x轴交于另一点
与x轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
![]() 求这条抛物线的表达式;
求这条抛物线的表达式;
![]() 在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
![]() 如图2,若点M在这条抛物线上,且
如图2,若点M在这条抛物线上,且![]() ,
,
![]() 求点M的坐标;
求点M的坐标;
![]() 在
在![]() 的条件下,是否存在点P,使得
的条件下,是否存在点P,使得![]() ∽
∽![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com