
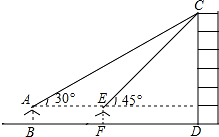
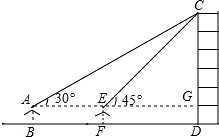
小敏同学测量一建筑物 CD 的高度,她站在 B 处仰望楼顶 C,测得仰角为 30°,再往建筑物方向 走 30m,到达点 F 处测得楼顶 C 的仰角为 45°(BFD 在同一直线上).已知小敏的眼睛与地面距离为 1.5m,求这栋建筑物 CD 的高度(参考数据: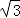 ≈1.732,
≈1.732, 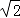 ≈1.414.结果保留整数)
≈1.414.结果保留整数)
【考点】解直角三角形的应用-仰角俯角问题.
【分析】延长 AE 交 CD 于点 G,设 CG=xm,在直角△CGE 中利用 x 表示出 EG,然后在直角△ACG
中,利用 x 表示出 AG,根据 AE=AG﹣EG 即可列方程求得 x 的值,进而球儿 CD 的长.
【解答】解:延长 AE 交 CD 于点 G.设 CG=xm, 在直角△CGE 中,∠CEG=45°,则 EG=CG=xm.
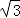 在直角△ACG 中,AG=
在直角△ACG 中,AG=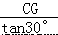 = xm.
= xm.
∵AG﹣EG=AE,
∴ 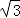 x﹣x=30, 解得:x=15(
x﹣x=30, 解得:x=15( 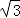 +1)≈15×2.732≈40.98(m). 则 CD=40.98+1.5=42.48(m).
+1)≈15×2.732≈40.98(m). 则 CD=40.98+1.5=42.48(m).
答:这栋建筑物 CD 的高度约为 42m.


科目:初中数学 来源: 题型:
下列命题中真命题有几个( )
①三角形的任意两边之和都大于第三边;②三角形的任意两角之和都大于第三个角;
③同位角都相等;④若 a=b,则|a|=|b|;⑤相等的角都是直角;
⑥同角的补角不一定相等;⑦一个三角形中最大的角不会小于 60°. A.1 个 B.2 个 C.3 个 D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
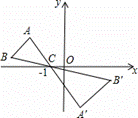
如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是
(﹣1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形
△A′B′C,并把△ABC的边长放大到原来的2倍.设B′的坐标是(3,-1),
则点B的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在边长为 1 的正方形网格中,△ABC 的三边 a,b,c 的大小关系是( )
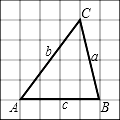
A.c<b<a B.c<a<b C.a<c<b D.a<b<c
查看答案和解析>>
科目:初中数学 来源: 题型:
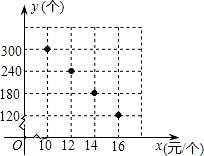
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得 利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量 y(个)与销售单价 x(元/个) 之间的对应关系如图所示:
(1)试判断 y 与 x 之间的函数关系,并求出函数关系式;
若许愿瓶的进价为 6 元/个,按照上述市场调查的销售规律,求销售利润 w(元)与销售单价 x(元/
个)之间的函数关系式;
(3)在的条件下,若许愿瓶的进货成本不超过 900 元,要想获得最大利润,试确定这种许愿瓶的销 售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的是( )
A.5m2n 与﹣4nm2 是同类项 B. 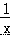 和
和 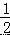 x 是同类项
x 是同类项
C.0.5x3y2 和 7x2y3 是同类项 D. 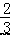 xyz 与
xyz 与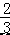 xy 是同类项
xy 是同类项
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com