
将矩形纸片 ABCD 按如图方式折叠,DE、CF 为折痕,折叠后点 A 和点 B 都落在点 O 处.若△EOF 是等边三角形,则 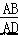 的值为 .
的值为 .
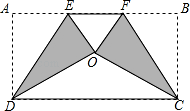
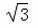 【考点】翻折变换(折叠问题).
【考点】翻折变换(折叠问题).
【专题】压轴题.
【分析】由△EOF 是等边三角形,可得 EF=OE=OF,∠OEF=60°,又由由折叠的性质可得:OE=AE, OF=BF,∠AED=∠OED,则可得 AB=3AE,∠AED=60°,则可证得 AD=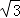 AE,继而求得答案.
AE,继而求得答案.
【解答】解:∵△EOF 是等边三角形,
∴EF=OE=OF,∠OEF=60°,
由折叠的性质可得:OE=AE,OF=BF,∠AED=∠OED,
∴AB=3AE,∠AED=  =60°,
=60°,
∵四边形 ABCD 是矩形,
∴∠A=90°,
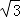 ∴tan∠AED=
∴tan∠AED= 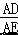 = ,
= ,
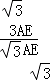 ∴AD= AE,
∴AD= AE,
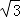 ∴
∴ 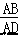 = = .
= = .
故答案为: .
【点评】此题考查了折叠的性质、等边三角形的性质、矩形的性质以及三角函数等知识.此题难度 适中,注意掌握折叠前后图形的对应关系,注意数形结合思想的应用.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
)如图,O为直线AB上一点,将直角三角板OCD的直角顶点放在点O处.
已知∠AOC的度数比∠BOD的度数的3倍多10°.
(1)求∠BOD的度数.
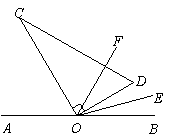 (2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
(2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
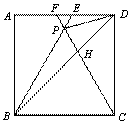 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.
给出下列结论:①△BDE∽△DPE;②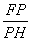 =
= 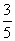 ;
;
③DP2=PH·PB; ④ 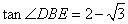 .
.
|
A. ①②③④ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线 y=﹣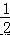 x2+
x2+ 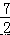 x 与矩形 OABC 的边 AB 交于点 D、B,A(0,3),C(6,0),则图中 抛物线与矩形 OABC 形成的阴影部分的面积的和为( )
x 与矩形 OABC 的边 AB 交于点 D、B,A(0,3),C(6,0),则图中 抛物线与矩形 OABC 形成的阴影部分的面积的和为( )
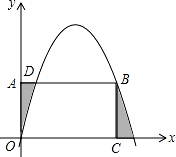
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
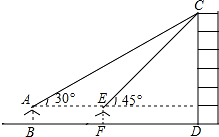
小敏同学测量一建筑物 CD 的高度,她站在 B 处仰望楼顶 C,测得仰角为 30°,再往建筑物方向 走 30m,到达点 F 处测得楼顶 C 的仰角为 45°(BFD 在同一直线上).已知小敏的眼睛与地面距离为 1.5m,求这栋建筑物 CD 的高度(参考数据: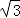 ≈1.732,
≈1.732, 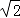 ≈1.414.结果保留整数)
≈1.414.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
某同学在计算多项式 M 加上 x2﹣3x+7 时,误认为是加上 x2+3x+7,结果得到答案是 5x2+6x﹣4.求:
(1)多项式 M; 这个问题的正确结果应是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com