
【题目】已知数轴上两点![]() 、
、![]() 对应的数分别为-1、3,点
对应的数分别为-1、3,点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() .
.
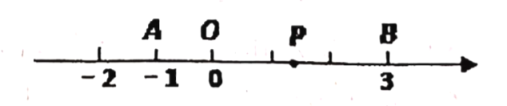
(1)若点![]() 到点
到点![]() 、点
、点![]() 的距离相等,则点
的距离相等,则点![]() 对应的数为 ;
对应的数为 ;
(2)利用数轴探究:找出满足![]() 的
的![]() 的所有值是 ;
的所有值是 ;
(3)当点![]() 以每秒6个单位长的速度从0点向右运动时,点
以每秒6个单位长的速度从0点向右运动时,点![]() 以每秒6个单位长的速度向右运动,点
以每秒6个单位长的速度向右运动,点![]() 以每秒钟5个单位长的速度向右运动,问它们同时出发,几秒后
以每秒钟5个单位长的速度向右运动,问它们同时出发,几秒后![]() 点到点
点到点![]() 、点
、点![]() 的距离相等?
的距离相等?
【答案】(1)1(2)-2或4(3)2秒或4秒
【解析】
(1)由点P到点A、点B的距离相等得点P是线段AB的中点,可确定点P对应的数;
(2)![]() 和
和![]() 分别表示P点到数轴上表示3和-1的点的距离,所以
分别表示P点到数轴上表示3和-1的点的距离,所以![]() 表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6,分P点在A点左侧和P点在B点右侧讨论计算.
表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6,分P点在A点左侧和P点在B点右侧讨论计算.
解:(1)∵点![]() 到点
到点![]() 、点
、点![]() 的距离相等,
的距离相等,
∴P点只能在A、B之间,
∴PA=PB=![]() AB=
AB=![]() ×4=2
×4=2
∴P点对应的数为1.
(2)![]() 表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6
表示P点到数轴表示3和-1的点的距离之和为6,即表示P点到A、B两点的距离之和为6
①当P在A点左侧时,PA+PB=6,即PA+PA+4=6,
∴PA=1,∴x==-2;
②当P在B点右侧时,PA+PB=6,即PB+4+PB=6,
∴PB=1,∴x=4
③当P点A、B之间时,x不存在.
∴x的值为-2或4.
(3)设t秒后![]() 点到点
点到点![]() 、点
、点![]() 的距离相等,
的距离相等,
当P点在B左侧时 5t+3-6t=1, ∴t=2
当P点在B右侧时6t-(5t+3)=1,∴t=4
所以它们出发2秒或4秒后P到A、B点的距离相等.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
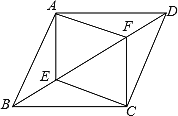
【题目】如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF.
(1)求证:AE=CF;
(2)连接AF、CE,判断四边形AECF的形状,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
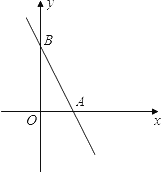
【题目】如图,直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.
轴相交于点B.
(1)求A、B两点的坐标;
(2)求△AOB的面积;
(3)若点P是![]() 轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
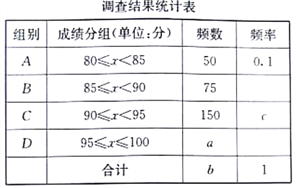
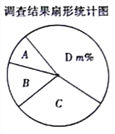
【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表。
根据以上信息解答下列问题
(1)统计表中,a= ,b= ,c= 。
(2)扇形统计图中,m的值为 。“C”所对应的圆心角的度数是 ;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
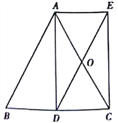
【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
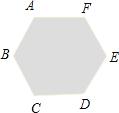
【题目】如图,在正六边形ABCDEF内放入2008个点,若这2008个点连同正六边形的六个顶点无三点共线,则该正六边形被这些点分成互不重合的三角形共_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的关联数.例如:若
的关联数.例如:若![]() ,则称
,则称![]() 与
与![]() 是关于2的关联数;
是关于2的关联数;
(1)若3与![]() 是关于2的关联数,则
是关于2的关联数,则![]() _______.
_______.
(2)若![]() 与
与![]() 是关于2的关联数,求
是关于2的关联数,求![]() 的值.
的值.
(3)若![]() 与
与![]() 是关于
是关于![]() 的关联数,
的关联数, ![]() ,
,![]() 的值与
的值与![]() 无关,求
无关,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
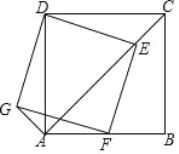
【题目】如图,正方形ABCD中,AB=4,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE、EF为邻边作矩 形DEFG,连接AG.
(1)求证:矩形DEFG是正方形;
(2)求AG+AE的值;
(3)若F恰为AB中点,连接DF交AC于点M,求ME的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com