
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.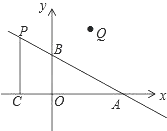
(1)当b=3时,
①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
【答案】
(1)解:①由A(4,0),B(0,3),
设直线AB解析式为y=kx+b,
把A与B坐标代入得: ![]() ,
,
解得:k=- ![]() ,b=3,
,b=3,
则直线AB解析式为y=- ![]() x+3;
x+3;
②∵QA=QO,OA=4,
∴xQ=2,
∵点P关于y轴的对称点为Q,
∴xP=-2,
代入直线AP解析式得- ![]() ×(-2)+3=
×(-2)+3= ![]() ,
,
则P坐标得P(-2, ![]() )
)
(2)解:①若∠QAC=90°,如图1所示,
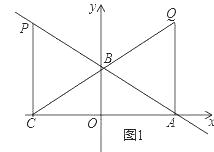
∴xQ=4,
∴a=xP=-4,
∴AC=AQ=8,即P(-4,8),
∴直线AP解析式为y=-x+4,
∴a=-4,b=4;
②若∠AQC=90°,如图2所示,
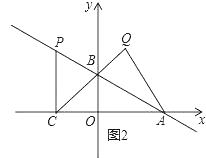
则AC=4-a=2CH=-4a,
∴a=- ![]() ,
,
∴xP=- ![]() ,yP=yq=
,yP=yq= ![]() ,即P(-
,即P(- ![]() ,
, ![]() ),
),
∴直线AP解析式为y=- ![]() x+2,
x+2,
∴a=- ![]() ,b=2,
,b=2,
综上所示,a=-4,b=4或a=- ![]() ,b=2
,b=2
【解析】(1)①由题意确定出B坐标,设直线AB解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可求出AB解析式;②由AQ=QO以及OA的长,确定出Q横坐标,根据P与Q关于y轴对称,得出P横坐标,代入直线AB解析式求出纵坐标,即可确定出P坐标;
(2)同时存在a、b,使得△QAC是等腰直角三角形,分两种情况考虑:①若∠QAC=90°;②若∠AQC=90°,分别求出a与b的值即可.
【考点精析】掌握确定一次函数的表达式是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


科目:初中数学 来源: 题型:
【题目】如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.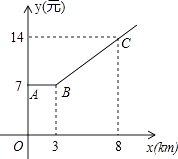
(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)某人乘坐13km,应付多少钱?
(3)若某人付车费42元,出租车行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.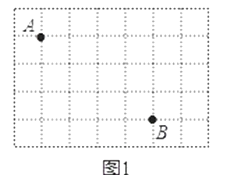
(1)在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(2)在图2中确定格点D使△ABD为等腰三角形,画出一个这样的△ABD;
(3)在图2中满足题(2)条件的格点D有个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①有理数和数轴上的点一一对应;
②成轴对称的两个图形是全等图形;
③- ![]() 是17的平方根;
是17的平方根;
④等腰三角形的高线、中线及角平分线重合.
其中正确的有( )
A.0个
B.1
C.2个
D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物园中有熊猫,孔雀,大象,梅花鹿四种可爱动物,为了解本班同学喜欢哪种动物的人最多,则调查的对象是( ).
A.本班的每一个同学
B.熊猫,孔雀,大象,梅花鹿
C.同学们的选票
D.记录下来的数据
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com