
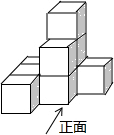
 如图是由多个完全相同的小正方体组成的几何体,其左视图是( )
如图是由多个完全相同的小正方体组成的几何体,其左视图是( )| A. | 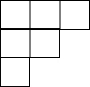 | B. | 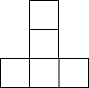 | C. | 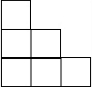 | D. | 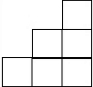 |
科目:初中数学 来源: 题型:选择题
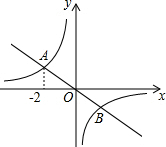 如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )
如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )| A. | (2,-1) | B. | (1,-2) | C. | ($\frac{1}{2}$,-1) | D. | (-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 摸出的2个球都是白球 | B. | 摸出的2个球有一个是白球 | ||
| C. | 摸出的2个球都是黑球 | D. | 摸出的2个球有一个黑球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
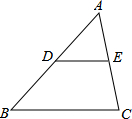 补充完整三角形中位线定理,并加以证明:
补充完整三角形中位线定理,并加以证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
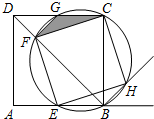 如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.
如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A、B),过B、C、E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com