
【题目】如图1,在平面直角坐标系xOy中,直线l经过点O,点A(0,6),经过点A、O、B三点的⊙P与直线l相交于点C(7,7),且CA=CB.
⑴ 求点B的坐标;
⑵ 如图2,将△AOB绕点B按顺时针方向旋转90°得到△A′O′B.判断直线![]() 与⊙P的位置关系,并说明理由.
与⊙P的位置关系,并说明理由.

【答案】⑴点B(8,0) ⑵ 直线A′O′与⊙P相切
【解析】试题分析:(1)过点C作CE⊥x轴于点E,过点C作CF⊥y轴于点F.
可以由已知坐标求出AF长,Rt△ACF≌Rt△BCE,可以求出BE=AF,得到OB长.
(2) AB的中点即为圆心P,取OB的中点R,连接RP并延长交A′O′的延长线于点Q,利用旋转条件,RP⊥A′O′.,最终得到四边形RBO′Q是矩形, 圆心P到直线A′O′的距离,和半径相等,所以可以得到直线A′O′与⊙P相切.
⑴ 过点C作CE⊥x轴于点E,过点C作CF⊥y轴于点F.
∴ ∠CFO=∠CEO=∠CEB=90°,∵ ∠AOB=90°,
∴ 四边形FOEC是矩形 ,
∴ ∠FCE=90° ,
∴ ∠ACE+∠ACF=90°,
由点C(7,7)得:CF=CE=7,
∴ ∠AOC=∠BOC=45°,OF=CE=7,OE=CF=7,
∴ ∠CBA=∠COA=45°,∠CAB=∠COB=45°,
∴ ∠CAB=∠CBA , ∴ AC=BC.
∵ 点A(0,6) ,∴ OA=6,
∴ AF=OF-OA=7-6=1 .
∵ ∠AOB=90° , ∴ AB为⊙P的直径 ,
∴ ∠ACB=90°,
∴ ∠ACE+∠BCE=90°,
∴ ∠ACF=∠BCE .
在Rt△ACF和Rt△BCE中,
![]() ,
,
∴ Rt△ACF≌Rt△BCE,
∴ BE=AF=1,
∴ OB=OE+EB=7+1=8,
∴ 点B(8,0) .
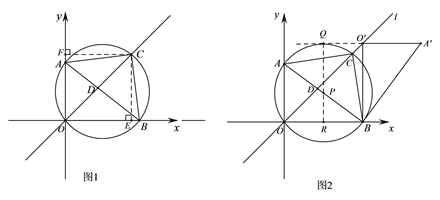
⑵ 直线A′O′与⊙P相切.
如图2,由AB是⊙P的直径可知:AB的中点即为圆心P,
取OB的中点R,连接RP并延长交A′O′的延长线于点Q,,
∴ PR∥OA,PR=![]() =3 ,
=3 ,
∵ ∠AOB=90° ∴ ∠QRB=90°,
∵ △A′O′B′由△AOB绕点B按顺时针方向旋转90°得到,
∴ ∠OBO′=90°,BO′=BO=8,
∵ ∠AO′B=90° ∴ ∠BO′Q=90° 即:RP⊥A′O′.
∴ 四边形RBO′Q是矩形,
∴ ∠O′QR=90°,RQ=BO′=8 ,
∴ PQ=RQ-PR=8-3=5,
∵ ⊙P的直径AB=10,
∴ 圆心P到直线A′O′的距离等于半径长5,
∴直线A′O′与⊙P相切.


科目:初中数学 来源: 题型:
【题目】据宜昌市统计局2013年底统计,中心城区人均住房建筑面积约为30平方米,为把宜昌市建设成特大城市,中心城区住房建筑面积和人口数都迅速增加.2014年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是a,2015年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是2a.从2014年开始,中心城区人口数在2013年180万的基础上每年递增m(m>0)万人,这样2015年中心城区的人口数比2014年中心城区人口数的1.5倍少80万人,已知2015年中心城区的人均住房建筑面积与2014年持平.
(1)根据题意填表(用含a,m的式子表示各个数量);
年份 | 中心城区人口数 | 中心城区人均住房建筑面积(单位:平方米) | 中心城区住房建筑面积(单位:万平凡米) |
2013年 | 180 | 30 | 5400 |
2014年 |
|
|
|
2015年 |
|
|
|
(2)求题目中的a和m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款工艺品,每件成本![]() 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,若销售单价每降低
件,若销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于
件,但要求销售单价不得低于![]() 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利![]() 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() (利润=售价﹣制造成本)
(利润=售价﹣制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是几次活动汇总后统计的数据:
摸球的次数s | 150 | 200 | 500 | 900 | 1000 | 1200 |
摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
摸到白球的频率 | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(1)请估计:当次数s很大时,摸到白球的频率将会接近 ;假如你去摸一次,你摸到白球的概率是 (精确到0.1).
(2)试估算口袋中红球有多少只?
(3)解决了上面的问题后请你从统计与概率方面谈一条启示.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com