
【题目】把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A顶着桌面,若另两个顶点分别距离桌面5cm和3cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离即DE的长为( )
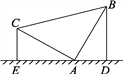
A. 4cm B. 6cm C. 8cm D. 求不出来
 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】探究题
(1)【证法回顾】
证明:三角形中位线定理.
已知:如图1,DE是△ABC的中位线.
求证:DE∥BC,DE= ![]() BC.
BC.
证明:添加辅助线:如图1,在△ABC中,延长DE (D、E分别是AB、AC的中点)到点F,使得EF=DE,连接CF;请继续完成证明过程: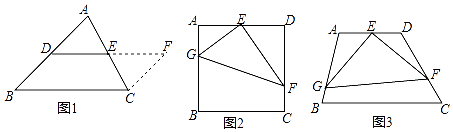
(2)【问题解决】
如图2,在正方形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若AG=2,DF=3,∠GEF=90°,求GF的长.
(3)【拓展研究】如图3,在四边形ABCD中,∠A=105°,∠D=120°,E为AD的中点,G、F分别为AB、CD边上的点,若AG=3 ![]() ,DF=2,∠GEF=90°,求GF的长.
,DF=2,∠GEF=90°,求GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2014年至2016年,中国同‘一带一路’沿线国家贸易总额超过3万亿美元”,将数据3万亿美元用科学记数法表示为( )
A.3×1014美元
B.3×1013美元
C.3×1012美元
D.3×1011美元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 在同一平面内,过一点有且只有一条直线与已知直线平行
B. 在同一平面内,过一点有且只有一条直线与已知直线垂直
C. 从直线外一点作这条直线的垂线段叫做点到这条直线的距离
D. 不相交的两条线段是平行线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°,若抛物线 y=x+k与扇形OAB的边界总有两个公共点,则实数取值范围是

A. -4<k<![]() B. -2<k<
B. -2<k<![]()
C. -4<k<![]() D. --2<k<
D. --2<k<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠C=90°,AB的垂直平分线MN交BC于点D.
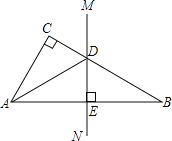
(1)如果∠CAD=20°,求∠B的度数;
(2)如果∠CAB=50°,求∠CAD的度数;
(3)如果∠CAD:∠DAB=1:2,求∠CAB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com