
【题目】已知,在△ABC中,∠ABC=90,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D.E.F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是( )
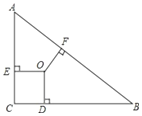
A. 2,2,2 B. 3,3,3 C. 4,4,4 D. 5,5,5
【答案】B
【解析】
由角平分线的性质易得OE=OF=OD,AE=AF,CE=CD,BD=BF,设OE=OF=OD=x,则CE=CD=x,BD=BF=15-x,AF=AE=8-x,所以15-x+8-x=17,解答即可.
解:如图,
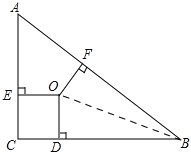
连接OB,
∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,
∴OE=OF=OD,
又∵OB是公共边,
∴Rt△BOF≌Rt△BOD(HL),
∴BD=BF,
同理,AE=AF,CE=CD,
∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,
∴OECD是正方形,
设OE=OF=OD=x,则CE=CD=x,BD=BF=15-x,AF=AE=8-x,
所以15-x+8-x=17
解得x=3.
则OE=OF=OD=3,
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例). 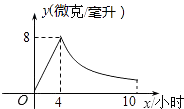
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于4微克/毫升的持续时间多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ截梯形为两个四边形.问当P,Q同时出发,几秒时其中一个四边形为平行四边形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.
(I)请填写下表
购买量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金额/元 | 0 | 250 | _ | 700 | __ | … |
(Ⅱ)写出付款金额关于购买量的函数解析式;
(Ⅲ)如果某人付款2100元,求其购买苹果的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若![]() >0,
>0,![]() >0,则
>0,则![]() >0;若
>0;若![]() <0,
<0,![]() <0,则
<0,则![]() >0;
>0;
(2)若![]() >0,
>0,![]() <0,则
<0,则![]() <0;若
<0;若![]() <0,
<0,![]() >0,则
>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则__________或__________.
<0,则__________或__________.
(3)根据上述规律,求不等式![]() 的解集.
的解集.
(4)试求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)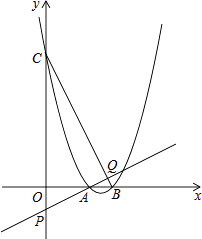
(1)当k= ![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 , C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC= ![]() ,则AF的长度为( )
,则AF的长度为( ) 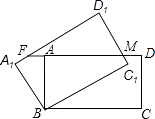
A.2﹣ ![]()
B.![]()
C.![]()
D.![]() ﹣1
﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com