
【题目】不等式 ![]() 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:解不等式2x﹣1≥1,得:x≥1,
解不等式x﹣2<0,得:x<2,
∴不等式组的解集为:1≤x<2,
故选:C.
【考点精析】认真审题,首先需要了解不等式的解集在数轴上的表示(不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈),还要掌握一元一次不等式组的解法(解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ))的相关知识才是答题的关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆. 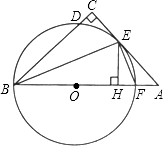
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠ABC=90,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D.E.F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是( )
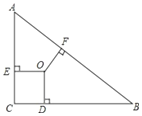
A. 2,2,2 B. 3,3,3 C. 4,4,4 D. 5,5,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区从2011年开始,组织全民健身活动,结合社区条件,开展了广场舞、太极拳、羽毛球和跑步四个活动项目,现将参加项目活动总人数进行统计,并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图,请你根据统计图解答下列题 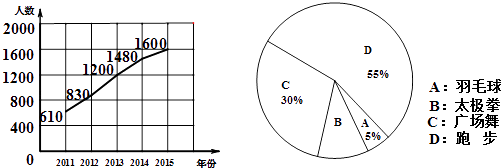
(1)2015年比2011年增加人;
(2)请根据扇形统计图求出2015年参与跑步项目的人数;
(3)组织者预计2016年参与人员人数将比2015年的人数增加15%,名各活动项目参与人数的百分比与2016年相同,请根据以上统计结果,估计2016年参加太极拳的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
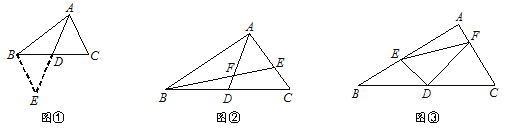
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com