练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

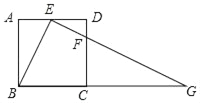
    【题目】如图，在正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=DC，连接EF并延长交BC的延长线于点G．

    （1）求证：△ABE∽△DEF；

    （2）若正方形的边长为4，求BG的长．

    【答案】（1）见解析（2）10

    【解析】

    （1）利用正方形的性质，可得∠A=∠D，根据已知条件可知,根据两边对应成比例且夹角相等三角形相似，可得△ABE∽△DEF；（2）根据平行线分线段成比例定理，可得CG的长，即可求出BG的长.

    （1）证明：∵四边形ABCD为正方形，

    ∴AD=AB=DC=BC, ∠A=∠D=90°，

    ∵AE=ED，

    ∴，

    又∵DF=DC，∴

    ∴

    ∴△ABE∽△DEF；

    （2）解：∵四边形ABCD为正方形，

    ED∥BG，

    ∴

    又∵DF=DC，正方形的边长为4，

    ∴ED=2，CG=6，

    BG=BC+CG=10.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某社区计划对面积为3600m2的区域进行绿化，经投标，由甲，乙两个工程队来完成,已知甲队4天能完成绿化的面积等于乙队8天完成绿化的面积，甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2

    (1)求甲、乙两工程队每天能完成绿化的面积；

    (2)若甲队每天化费用是1.2万元，乙队每天绿化费用为0.5万元，要使这次绿化的总费用不超过40万元，则至少应安排乙工程队绿化多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为响应荆州市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m长的栅栏围成．设矩形ABCD空地中，垂直于墙的边AB=xm，面积为ym2（如图）．

    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；

    （2）若矩形空地的面积为160m2，求x的值；

    （3）若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵（每种植物的单价和每棵栽种的合理用地面积如下表）．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．

    甲

    乙

    丙

    单价（元/棵）

    14

    16

    28

    合理用地（m2/棵）

    0.4

    1

    0.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在学习三角形的知识时, 发现如下三个有趣的结论：

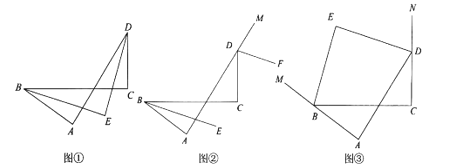
    (1)如图①, ∠A＝∠C＝90°, ∠ABC的平分线与∠ADC的平分线交于点E, 则BE、DE的位置关系是 ；

    (2)如图②, ∠A＝∠C＝90°, BE平分∠ABC, DF平分∠ADC的外角, 则BE与DF的位置关系是 ；

    (3)如图③, ∠A=∠C＝90°, ∠ABC的外角平分线与∠ADC的外角平分线交于点E, 则BE、DE的位置关系是 . 请你完成命题 (3)证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

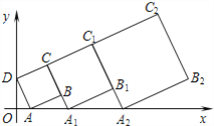
    【题目】在平面坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1,………按这样的规律进行下去，正方形A2018B2018C2018C2017的面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD中，∠A=140°，∠D=80°.

    (1)如图1，若∠B=∠C，试求出∠C的度数；

    (2)如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抚顺市某校想知道学生对“遥远的赫图阿拉”，“旗袍故里”等家乡旅游品牌的了解程度，随机抽取了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必选且只选一项）A．十分了解，B．了解较多，C．了解较少，D．不知道．将调查的结果绘制成如下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：

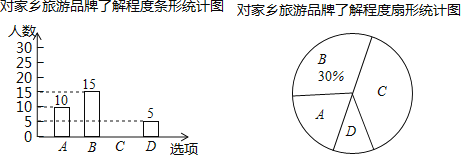
    （1）本次调查了多少名学生？

    （2）补全条形统计图；

    （3）该校共有500名学生，请你估计“十分了解”的学生有多少名？

    （4）在被调查“十分了解”的学生中有四名学生会干部，他们中有3名男生和1名女生，学校想从这4人中任选两人做家乡旅游品牌宣传员，请用列表或画树状图法求出被选中的两人恰好是一男一女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知△ABC和△BDE都是等边三角形。则下列结论：①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60.⑤△BFG是等边三角形，其中正确的有___.

    查看答案和解析>>

    同步练习册答案