
����Ŀ����ͼ1���ھ���ABCD�У�AB=4��AD=2����P�DZ�AB�ϵ�һ�����㣨�����A����B�غϣ�����Q�ڱ�AD�ϣ�����CBP�͡�QAP�ֱ���PC��PQ�۵���ʹB����E���غϣ�A����F���غϣ���P��E��F���㹲�ߣ�
��1������Eƽ���߶�PF�����ʱAQ�ij�Ϊ���٣�
��2�����߶�CE���߶�QF���ڵ�ƽ��ֱ��֮��ľ���Ϊ2�����ʱAP�ij�Ϊ���٣�
��3���ڡ��߶�CE�������߶�QF��������A���������У��Ƿ����������ͬһ��ֱ���ϵ�����������ڣ������ʱAP�ij����������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�ɡ�CBP�͡�QAP�ֱ���PC��PQ�۵����õ���QFP�͡�PCE�����AQP�ա�FQP����CPB�ա�CPE
��PA=PF��PB=PE����QPA=��QPF����CPB=��CPE��
��EF=EP��
��AB=AP+PB=FP+PB=EF+EP+PB=3PB��
��AB=4��
��PB= ![]() ��
��
��AP= ![]() ��
��
��180��=��QPA+��QPF+��CPB+��CPE=2����QPA+��CPB����
���QPA+��CPB=90�㣮
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬
���CPB+��PCB=90�㣬
���QPA=��PCB��
�ڡ�QAP�͡�PBC�У�
![]() ��
��
���QAP�ס�PBC��
�� ![]() ��
��
�� ![]() ��
��
�� ![]()
��2��
�⣺�����⣬��PF=EP+2��EP=FP+2��
��EP��PF=2ʱ��
��EP=PB��PF=AP��
��PB��AP=2��
��AP+PB=4��
��2BP=6��
��BP=3��
��AP=1��
��PF��EP=2ʱ��
��EP=PB��PF=AP��
��AP��PB=2��
��AP+PB=4��
��2AP=6��
��AP=3��
��AP�ij�Ϊ1��3��
��3��
�⣺����CE���A��ͬһֱ���ϣ���ͼ2������AC����E��AC�ϣ�
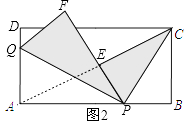
�ڡ�AEP�͡�ABC�У�
![]() ��
��
���AEP�ס�ABC��
�� ![]() ��
��
��AP=x����EP=BP=4��x��
��Rt��ABC��
��AB=4��BC=2��
��AC=2 ![]() ��
��
�� ![]() ��
��
��� ![]() ��
��
����CE��QF��ͬһֱ���ϣ���ͼ3��
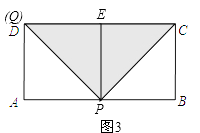
�ߡ�AQP�ա�EQP����CPB�ա�CPE��
��AP=EP=BP��
��2AP=4��
��AP=2��
����������1����������Ҫ��ʾ��ͼ����ͼ�����۵�֪����AQP�ա�FQP����CPB�ա�CPE����������AB�ߵĹ�ϵ֪����Eƽ��FP����BP= ![]() ��AP=
��AP= ![]() ������֪������CP��QP�����QAP�ס�PBC�����ɱ�֮��ijɱ����ù���AQ�ķ��̣�������ɣ���2���ɣ�1����EP=BP��FP=AP��PB+AP=10���߶�CE���߶�QF���ڵ�ƽ��ֱ��֮��ľ���Ϊ2���ʾEF=2���������ֿ��ܣ�PF=EP+2��EP=FP+2�����ǵõ�������ϵʽ���ý��ۣ���3�����߶�CE�������߶�QF��������A�������ߣ�˼����P�˶�����ֽ�ص㣬QF������A���ߣ���CE��QF����ʱ��P��ǡΪAB�е㣬��ͼ�����߶ζ���CD�ϣ���CE��A����ʱ�������ӶԽ���AC��CE��AC�ϣ���ʱ��AEP�ס�ABC������AP�ij��ã�
������֪������CP��QP�����QAP�ס�PBC�����ɱ�֮��ijɱ����ù���AQ�ķ��̣�������ɣ���2���ɣ�1����EP=BP��FP=AP��PB+AP=10���߶�CE���߶�QF���ڵ�ƽ��ֱ��֮��ľ���Ϊ2���ʾEF=2���������ֿ��ܣ�PF=EP+2��EP=FP+2�����ǵõ�������ϵʽ���ý��ۣ���3�����߶�CE�������߶�QF��������A�������ߣ�˼����P�˶�����ֽ�ص㣬QF������A���ߣ���CE��QF����ʱ��P��ǡΪAB�е㣬��ͼ�����߶ζ���CD�ϣ���CE��A����ʱ�������ӶԽ���AC��CE��AC�ϣ���ʱ��AEP�ס�ABC������AP�ij��ã�
�����㾫����������Ĺؼ��������ⷭ�۱任���۵����⣩�����֪ʶ�������۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���ȣ��Լ������������ε����ʵ����⣬�˽��Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���������н��ۣ� ��b2=4ac����abc��0����a��c����4a��2b+c��0��������ȷ�ĸ����У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0����ͼ���һ���֣������ߵĶ���������A��1��3������x���һ��������B��4��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ� ��abc��0���ڷ���ax2+bx+c=3��������ȵ�ʵ����������������x�����һ�������ǣ���1��0�����ܵ�1��x��4ʱ����y2��y1����x��ax+b����a+b��������ȷ�Ľ����� �� ��ֻ��д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA��OB������ֱ��������CDE����CD��OB�ϣ���ECD=45�㣬��������CDE�Ƶ�C��ʱ����ת75�㣬��E�Ķ�Ӧ��Nǡ������OA�ϣ��� ![]() ��ֵΪ�� ��
��ֵΪ�� �� 
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ�ߺ�Բ�������������������и���һ����Ϊ�����ε����Σ������ε��ĸ����㶼�ھ��εı��ϣ������ͬ��ͼ����Ϊͬһ�֣���������ͼ�ۼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����װ���ĸ��ֱ�������֩�1����2����3����4��С�����ǵ���״����С���ʵص���ȫ��ͬ��Сǿ�ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy��
��1�����б�������״ͼ��ʾ����x��y�������п��ܳ��ֵĽ����
��2����Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���y=x��1ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���Ȩƽ����ʱ��ͳ���г��ø��������ֵ���������ʵ�����ݣ��Ѹ����Ƶ��������Ӧ����ֵ��Ȩ��������������֪ʶ����������ʵ�����⣮
Ϊ�˽�5·������������Ӫ�������������ͳ����ij��5·��������ÿ�����а�ε��ؿ����������ؿ����Ķ��ٷֳ�A��B��C��D���飬�õ�����ͳ��ͼ��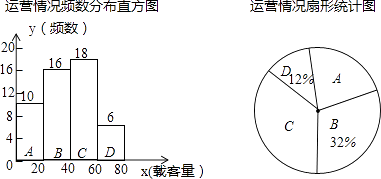
��1����A���Ӧ����Բ�ĽǵĶ�������д�������ؿ�������λ�����ڵ��飻
��2��������5·��������ƽ��ÿ����ؿ�����
��3�����һ���°�30����㣬�����5·��������һ���µ����ؿ��������ѽ���ÿ�ѧ��������ʾ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=5���Խ���AC=6��������A��AE��BC������ΪE����AE�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߶�AB��ͬ��������AM��BN������MAB���NBA��ƽ���߷ֱ�����BN��AM�ڵ�E��F��AE��BF���ڵ�P����ͼ�����ͬѧ���ֵ�����AM��BN���ڵ�C���ҡ�ACB=60��ʱ���������������ۣ�
�١�APB=120�㣻��AF+BE=AB��
��ô����AM��BNʱ��
��1����㷢�ֵĽ��ۻ��������������������֤���������������������APB�Ķ�����д��AF��BE��AB����֮��ĵ�����ϵ��������֤����
��2�����QΪ�߶�AE��һ�㣬QB=5����AF+BE=16���ı���ABEF�����Ϊ32 ![]() ����AQ�ij���
����AQ�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com