
【题目】解方程
(1)4(x﹣1)=1﹣x
(2)![]() .
.
【答案】
(1)解:去括号得:4x﹣4=1﹣x,
移项合并得:5x=5,
解得:x=1
(2)解:去分母得:2x+2﹣5x+1=6,
移项合并得:﹣3x=3,
解得:x=﹣1
【解析】(1)先去括号(括号外的4要与括号里的每一项都要相乘,不能漏乘),再移项合并同类项,然后将未知数系数化为1,即可求解。
(2)先去分母(两边同时乘以6,右边的1也要乘以6,不能漏乘),再去括号(括号前是负号,去掉括号和负号,括号里的每一项都要变号。),然后移项合并同类项,最后把未知数的系数化为1。
【考点精析】根据题目的已知条件,利用等式和解一元一次方程的步骤的相关知识可以得到问题的答案,需要掌握等式两边同时加上或减去或乘以或除以(不为0)一个代数式,所得结果仍是等式;先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E.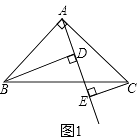
(1)求证:BD=DE+CE;
(2)若直线AE绕A点旋转到图2位置时(BD<CE),其余条件不变,则BD与DE、CE的数量关系如何?请予以证明;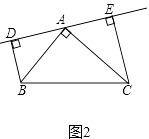
(3)若直线AE绕A点旋转到图3位置时(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不需说明理由;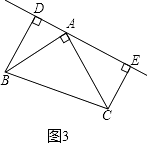
(4)根据以上的讨论,请用简洁的语言表述BD与DE、CE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将方程3x(x﹣1)=5(x+2)化为一元二次方程的一般式,正确的是( )
A.4x2﹣4x+5=0B.3x2﹣8x﹣10=0C.4x2+4x﹣5=0D.3x2+8x+10=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC. 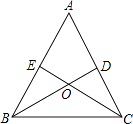
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=![]() 的图象经过D点.
的图象经过D点.

(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y=![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com