Question

【题目】已知：射线在的内部，，，平分．

（1）如图，若点，，在同一条直线上，是内部的一条射线，请根据题意补全图形，并求的度数；

（2）若，直接写出的度数（用含的代数式表示）．

Answer 1

【答案】（1）图详见解析，；（2）当射线在的内部时，； 当射线在的外部时，．

【解析】

（1）作出∠AOD的平分线OE，根据∠AOC:∠BOC=8:1求出∠BOC=20°，依据∠COD=2∠COB得∠COD=40°，从而可求∠AOD=120°，根据OE平分∠AOD得∠DOE=60°,从而可求出的度数；

（2）分两种情况考虑：当射线在的内部时，；当射线在的外部时，．

（1）补全图形，如图所示：

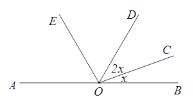
∵点，，在同一条直线上，

∴(平角的定义) ．

∵，

∴， ．

∵，

∴．

∴．

∵平分，

∴(角平分线的定义)．

∴

（2）①当射线在的内部时，如图，

∵，

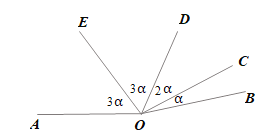
∴∠AOC=8α，

∵

∴

∴∠AOD=∠AOC-∠COD=6α,

∵平分

∴∠DOE=∠AOD=3α，

∴∠COE=∠COD+∠DOE=2α+3α=5α；

当射线在的外部时，如图，

∵，

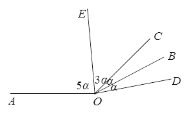
∴∠AOC=8α，

∵

∴，∠BOD=α

∴∠AOD=∠AOC+∠COD=10α,

∵平分

∴∠DOE=∠AOD=5α，

∴∠COE=∠DOE -∠COD =5α-2α=3α.