
【题目】课本107页,画∠AOB的角平分线的方法步骤是:
①以O为圆心,适当长为半径作弧,交OA于M点,交OB于N点;
②分别以M,N为圆心,大于 ![]() MN的长为半径作弧,两弧在∠AOB的内部相交于点C;
MN的长为半径作弧,两弧在∠AOB的内部相交于点C;
③过点C作射线OC.
射线OC就是∠AOB的角平分线.
请你说明这样作角平分线的根据是( )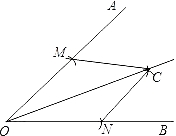
A.SSS
B.SAS
C.ASA
D.AAS
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)当a=2时,解答下列问题:
①QB= ,PD= .(用含t的代数式分别表示)
②通过计算说明,不存在t的值使得四边形PDBQ为菱形.
(2)当a为某个数值时,四边形PDBQ在某一时刻为菱形,求a的值及四边形PDBQ为菱形时t的值.
(3)当t=2时,在整个运动过程中,恰好存在线段PQ的中点M到△ABC三边距离相等,直接写出此刻a的值.
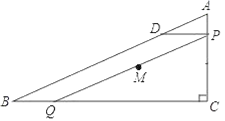
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBD是等腰三角形,EB=ED;
②折叠后∠ABE和∠CBD一定相等;
③折叠后得到的图形是轴对称图形;
④△EBA和△EDC一定是全等三角形.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图:
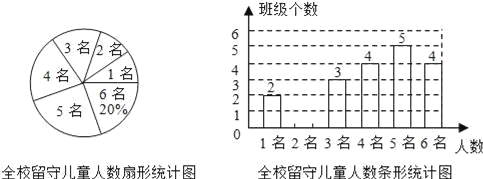
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com