
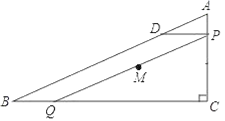
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����P�ӵ�A�����ر�AC���C��ÿ��1����λ���ȵ��ٶ��˶���ͬʱ��Q�ӵ�C�����ر�CB���B��ÿ��a����λ���ȵ��ٶ��˶�������P��PD��BC����AB�ڵ�D������PQ��������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����a=2ʱ������������⣺
��QB=�� ����PD=�� �������ú�t�Ĵ���ʽ�ֱ��ʾ��
��ͨ������˵����������t��ֵʹ���ı���PDBQΪ���Σ�
��2����aΪij����ֵʱ���ı���PDBQ��ijһʱ��Ϊ���Σ���a��ֵ���ı���PDBQΪ����ʱt��ֵ��
��3����t=2ʱ���������˶������У�ǡ�ô����߶�PQ���е�M����ABC���߾�����ȣ�ֱ��д���˿�a��ֵ��
���𰸡���1����8��2t��![]() t���ڲ����ڣ����ɼ�������
t���ڲ����ڣ����ɼ�������
��2������![]() �룬�ı���PDBQ�����Σ�
�룬�ı���PDBQ�����Σ�
��3������������a��ֵΪ2��
�������������������1���ٸ�������ã�CQ=2t��PA=t����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD��BC�����ɵ�tanA=![]() =
=![]() =
=![]() ��������QB��PD��ֵ��
��������QB��PD��ֵ��
������APD�ס�ACB���������AD��BD�ij�����BQ��DP���ɵõ�BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�������ô�ʱDP��BD�ij�����DP��BD�����ж�PDBQ����Ϊ���Σ�
��2�����Q���ٶ�Ϊÿ��v����λ���ȣ���Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ���з��̼�����ô𰸣�
��3��������AP=2��PC=4��CQ=2a����QM=PM����M����ABC�����߾�����ȣ��Ƴ�CM�ǡ�PCQ��ƽ���ߣ��Ƴ�PC=CQ���ɵ�2a=4���Ƴ�a=2�������飬��ʱ��M����ABC�����ģ��ɴ˼��ɽ�����⣻
�����������1���ٸ�������ã�CQ=2t��PA=t��
��QB=8��2t��
����Rt��ABC�У���C=90�㣬AC=6��BC=8��PD��BC��
���APD=90�㣬
��tanA=![]() =
=![]() =
=![]() ��
��
��PD=![]() t��
t��
�ʴ�Ϊ����1��8��2t��![]() t��
t��
�ڲ�����
��Rt��ABC�У���C=90�㣬AC=6��BC=8��
��AB=10
��PD��BC��
���APD�ס�ACB��
��![]() =
=![]() ����
����![]() =
=![]() ��
��
��AD=![]() t��
t��
��BD=AB��AD=10��![]() t��
t��
��BQ��DP��
�൱BQ=DPʱ���ı���PDBQ��ƽ���ı��Σ�
��8��2t=![]() ����ã�t=
����ã�t=![]() ��
��
��t=![]() ʱ��PD=
ʱ��PD=![]() ��
��![]() =
=![]() ��BD=10��
��BD=10��![]() ��
��![]() =6��
=6��
��DP��BD��
��PDBQ��������
��2�����Q���ٶ�Ϊÿ��v����λ���ȣ�
��BQ=8��vt��PD=![]() t��BD=10��
t��BD=10��![]() t��
t��
Ҫʹ�ı���PDBQΪ���Σ���PD=BD=BQ��
��PD=BDʱ����![]() t=10��
t=10��![]() t����ã�t=
t����ã�t=![]() ��
��
��PD=BQ��t=![]() ʱ����
ʱ����![]() ��
��![]() =8��
=8��![]() v����ã�v=
v����ã�v=![]() ��
��
����Q���ٶ�Ϊÿ��![]() ����λ����ʱ������
����λ����ʱ������![]() �룬�ı���PDBQ�����Σ�
�룬�ı���PDBQ�����Σ�
��3��������AP=2��PC=4��CQ=2a��
��QM=PM����M����ABC�����߾�����ȣ�
��CM�ǡ�PCQ��ƽ���ߣ�
��PC=CQ��
��2a=4��
��a=2�������飬��ʱ��M����ABC�����ģ�
������������a��ֵΪ2��


 �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
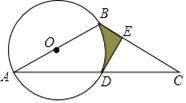
����Ŀ����ͼ����O��ֱ��AB=4����BAC=30�㣬AC����O��D��D��AC���е㣮
��1������D��DE��BC������ΪE����֤��ֱ��DE�ǡ�O�����ߣ�
��2����![]() ���߶�DE��BEΧ�ɵ���Ӱ�����
���߶�DE��BEΧ�ɵ���Ӱ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
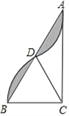
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=4![]() ���Ե�CΪԲ�ģ�CB�ij�Ϊ�뾶��������AB�߽��ڵ�D����
���Ե�CΪԲ�ģ�CB�ij�Ϊ�뾶��������AB�߽��ڵ�D����![]() �Ƶ�D��ת180����B���Aǡ���غϣ���ͼ����Ӱ���ֵ����Ϊ_____��
�Ƶ�D��ת180����B���Aǡ���غϣ���ͼ����Ӱ���ֵ����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и����߶��У�����������ε��ǣ�������
A. 1cm��2cm��3cm B. 2cm��3cm��4cm
C. 1cm��8cm��4cm D. 4cm��4cm��8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���α�107ҳ������AOB�Ľ�ƽ���ߵķ��������ǣ�
����OΪԲ�ģ��ʵ���Ϊ�뾶��������OA��M�㣬��OB��N�㣻
�ڷֱ���M��NΪԲ�ģ����� ![]() MN�ij�Ϊ�뾶�����������ڡ�AOB���ڲ��ཻ�ڵ�C��
MN�ij�Ϊ�뾶�����������ڡ�AOB���ڲ��ཻ�ڵ�C��
�۹���C������OC��
����OC���ǡ�AOB�Ľ�ƽ���ߣ�
����˵����������ƽ���ߵĸ����ǣ� ��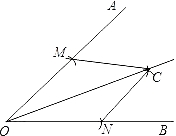
A.SSS
B.SAS
C.ASA
D.AAS
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.6a23ab=9a3b
B.��2ab2������2ab��=��4a2b3
C.��ab��2����a2b��=��a3b3
D.����3a2b������3ab��=��6a3b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ABCD��,�Խ���AC,BD�ཻ�ڵ�O,E,F�ǶԽ���AC�ϵ�����,����E,F���������ĸ�����ʱ,�ı���DEBF��һ����ƽ���ı���( )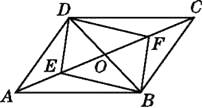
A.OE=OF
B.DF=BE
C.AE=CF
D.��AEB=��CFD
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com