
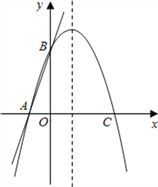
����Ŀ����ͼ��ֱ��y=kx+b��x���ڵ�A����1��0������y���ڵ�B��0��4������A��B����������߽�x������һ��C��
��1����ֱ��AB�Ľ���ʽ��
��2���ڸ������ߵĶԳ�������һ����P������PA��PB�������PA+PB����СֵΪ5�����ʱ�����ߵĽ���ʽ����P�����ꣻ
��3���ڣ�2�������£��������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ABQ�ǵ��������Σ������ڣ�ֱ��д����������������Q������ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=4x+4����2��y=-![]() x2+
x2+![]() x+4��P��1��
x+4��P��1��![]() ������3�����������ĵ�Q��ʹ��ABQΪ���������Σ�Q1��1��
������3�����������ĵ�Q��ʹ��ABQΪ���������Σ�Q1��1��![]() ����Q2��1��0����Q3��1��
����Q2��1��0����Q3��1��![]() ����Q4��1����
����Q4��1����![]() ����
����
����������������1������A��B���������ֱ�߽���ʽ�����k��b��ֵ���̶��ó�ֱ�ߵĽ���ʽ��
��2������BC����BC��Գ���Ľ��㼴��P���λ��������PA+PB����СֵΪ5�������OC�����ô���ϵ��������������߽���ʽ��ֱ��BC����ʽ���������P�����ꣻ
��3������������ĵ�Q��������Ϊ��1��y����Ȼ������������������QA=QB����BA=BQ����AB=AQ���ֱ����y��ֵ�ɵó���Q���꣮
��⣺(1)����A(1��0)����B(0��4)����ֱ��y=kx+b
�ã�![]() ��
��
��ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪy=4x+4��
(2)�ߵ�A����C���������ߵĶԳ���Գ�����PA+PB����СֵΪ�߶�BC�ij���
��BC=5��
��Rt��BOC����BC=5��BO=4��
��OC=![]() ��
��
���C������Ϊ(3��0)��
�������ߵĽ���ʽΪy=a(x+1)(x3)��
����B(0��4)����ã�a=![]() ��
��
�������ߵĽ���ʽΪ��y=![]() (x+1)(x3)=
(x+1)(x3)=![]() x2+
x2+![]() x+4��
x+4��
��ֱ��BC�Ľ���ʽΪy=mx+n��
����B(0��4)����C(3��0)����ɵ���
![]() ��
��
��ã�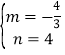 ��
��
��ֱ��BC�Ľ���ʽΪ��y=![]() x/span>+4��
x/span>+4��
�֡������ߵĶԳ���Ϊx=1��
�൱x=1ʱ��y=![]() ��
��
���P������Ϊ(1��![]() ).
).
(3)���������ĵ�Q��ʹ��ABQΪ����������.
��Q(1��y)��
�����������
�ٵ�QA=QBʱ������12+(y4)2=(11)2+y2��
��ã�y=![]() ����Q(1��
����Q(1��![]() )��
)��
�ڵ�BA=BQʱ����֪Q(1��0)��Q(1��8)(������������ȥ)��
�۵�AB=AQʱ��Q(1��![]() )��Q(1��
)��Q(1��![]() ).
).
��������������Q���ĸ���Q1��1��![]() ����Q2��1��0����Q3��1��
����Q2��1��0����Q3��1��![]() ����Q4��1����
����Q4��1����![]() ����
����


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��������ͬʱ�����330ǧ�ļס�������������У�s��ǧ�ף���ʾ������صľ��룬t���֣���ʾ������ʻ��ʱ�䣬��ͼ��L1��L2�ֱ��ʾ����������s��t�Ĺ�ϵ��
��1��L1��ʾ�����������صľ�������ʻʱ��Ĺ�ϵ��
��2������B���ٶ��Ƕ��٣�
��3����L1��L2�ֱ��ʾ������������s��t�Ĺ�ϵʽ��
��4��2Сʱ������������ǧ�ף�
��5����ʻ�ʱ���A��B����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
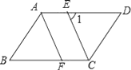
����Ŀ����ͼ����ABCD�У�CEƽ����BCD���ҽ�AD�ڵ�E��AF��CE���ҽ�BC�ڵ�F��
��1����֤����ABF�ա�CDE��
��2����ͼ������B=52��������1�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���������Ѽ����24km��С��8��00�Ӽҳ����������г�ȥ���Ѽң�����8��30�Ӽҳ������˳�����ͬ·��ȥ���Ѽң���ͬһֱ������ϵ�У�С����������н�·��S��km���뱱��ʱ��t��ʱ���ĺ���ͼ����ͼ��ʾ������ͼ��õ�С�����ۣ����д�����ǣ� ��
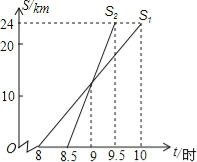
A. С�������г���ƽ���ٶ���12km/h
B. �����С����ǰ0.5Сʱ�������Ѽ�
C. �����ھ��12km����С��
D. 9��30��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
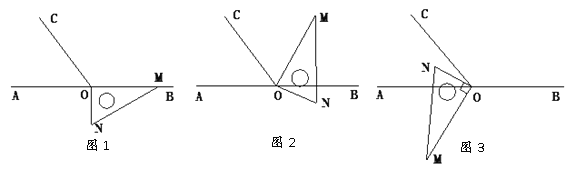
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=112��.��һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·�.
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC���ʣ�ֱ��ON�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��2����ͼ1�е����ǰ��Ƶ�O��ÿ��4����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC����t��ֵΪ���٣�
��3����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ�����̽������AOM���NOC֮���������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
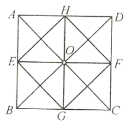
����Ŀ����ͼ����ͼ�����ɿ����ǻ���ͼ�Ρ�______����______��ƽ�Ƶõ��ģ�Ҳ�ɿ����ǻ���ͼ�Ρ�______����������ת______�εõ������ɿ����ǻ���ͼ�Ρ�______������ԳƵõ�����ͼ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��a��bΪ������������˵�������� a��b��Ϊ�෴������![]() ������
������![]() ��
��![]() ������
������![]() ����
����![]() ������
������![]() ����
����![]() ������.������ȷ����
������.������ȷ����
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
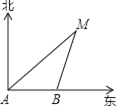
����Ŀ������9ʱ��һ������A����������ÿСʱ40������ٶ������������У�9ʱ30�ֵ���B������ͼ������A��B�����ֱ���С��M�ڱ�ƫ��45���ͱ�ƫ��15��������ô��B������С��M�ľ���Ϊ��������
A. 20���� B. 20![]() ���� C. 10
���� C. 10![]() ���� D. 20
���� D. 20![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
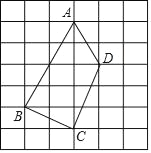
����Ŀ����ͼ���Ǵ�С��ȵı߳�Ϊ1�������ι��ɵ�����A��B��C��D��Ϊ��㣮
������ACD�����Ϊ_____��
��������ֻ���̶ȵ�ֱ�ߣ������߶�AD����һ��P��������BP��ʹ��ֱ��BP���ı���ABCD�������Ϊ1��2�����֣���ͼ�л����߶�BP�����ں����ϼ�Ҫ˵�������ͼ������_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com