Question

20．如图，△ABC的三个顶点坐标分别为（0，2），（-3，0）和（4，0），动点P从原点O出发（点P不与点O重合），沿着x轴的正方向以每秒1个单位的速度匀速运动，过点P作直线l⊥x轴，设点P的运动时间为t（秒）
（1）操作：
①在图中画出△ABO以点O为旋转中心顺时针旋转90°的图形（记为△A′B′O′）．
②在图中画出△A′B′O′关于直线l对称的图形（记为△A″B″O″）．
（2）设△A″B″O″与△ABC重叠部分的面积为S，求S与t的函数关系式，并写出t的取值范围．

Answer 1

分析 （1）根据旋转、轴对称的定义可以画出图象．
（2）根据待定系数法求出直线A″B″（用t表示），利用方程组解求点M坐标，根据平行成比例求点N的坐标（用t表示），分3种情形画出图象就可以求重叠部分面积．

解答 解：（1）答案见下图．△A′OB′，△A″O″B″就是所画．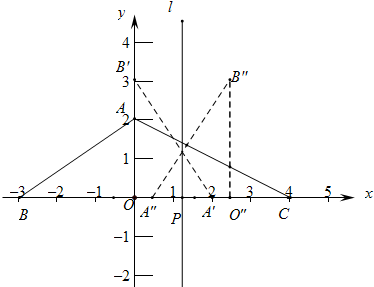

（2）由题意B″（2t，3），A″（2t-2，0），
设直线A″B″为y=kx+b，A、B代入得$\left\{\begin{array}{l}{2tk+b=3}\\{（2t-2）k+b=0}\end{array}\right.$解是$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=3-3t}\end{array}\right.$，
∴直线A″B″为y=$\frac{3}{2}x$+3-3t，
∵直线A″B″经过点A（0，2）时，t=$\frac{1}{3}$，
∴0＜t$\frac{1}{3}$时，如右图，
∵A（0，2），B（-3，0），
∴直线AB为y=$\frac{2}{3}X$+2，
由$\left\{\begin{array}{l}{y=\frac{2}{3}x+2}\\{y=\frac{3}{2}x+3-3t}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{18t-6}{5}}\\{y=\frac{12t+8}{5}}\end{array}\right.$，
∴M（$\frac{18t-6}{5}$，$\frac{12t+8}{5}$）．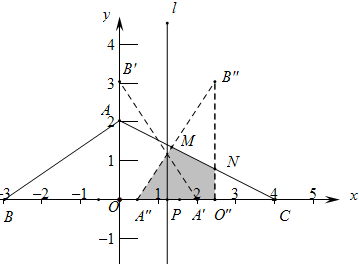
∵ON∥AO，
∴$\frac{ON}{AO}$=$\frac{CO″}{CO}$，
∴$\frac{ON}{2}=\frac{4-2t}{4}$，
∴ON=2-t，
∴S_重叠=S_△ABC-S_△BA″M-S_△CNO△″=7-$\frac{1}{2}$•[3-（2-2t）]-$\frac{1}{2}$•（4-2t）•（2-t）=-$\frac{3}{2}{t}^{2}$+3t+$\frac{5}{2}$．
当$\frac{1}{3}$＜t＜2时，如右图，
∵A（0，2），C（4，0），
∴直线AC为y=-$\frac{1}{2}$x+2，
由$\left\{\begin{array}{l}{y=-\frac{1}{2}x+2}\\{y=\frac{3}{2}x+3-3t}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{3t-1}{2}}\\{y=\frac{9-3t}{4}}\end{array}\right.$，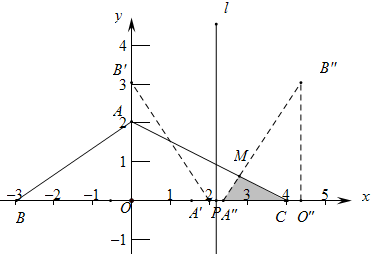
∴M（$\frac{3t-1}{2}$，$\frac{9-3t}{4}$），
∴S_重合=S_△A″CM-S_△CO″N=$\frac{1}{2}$•[4-（2t-2）]•$\frac{9-3t}{4}$-$\frac{1}{2}$•（4-2t）（2-t）=-$\frac{1}{4}$t²+t-$\frac{7}{4}$．

当3＜t＜4时，如右图，
S_重合=$\frac{1}{2}$[2-（2t-4）]•$\frac{9-3t}{4}$=$\frac{3}{4}$t²-$\frac{9}{2}t$+$\frac{27}{4}$，
综上所述S_重合=$\left\{\begin{array}{l}{-\frac{3}{2}{t}^{2}+3t+\frac{5}{2}}&{（0＜t≤\frac{1}{3}）}\\{-\frac{1}{4}{t}^{2}+t-\frac{7}{4}}&{（\frac{1}{3}＜t≤2）}\\{\frac{3}{4}{t}^{2}-\frac{9}{2}t+\frac{27}{4}}&{（2＜t≤4）}\end{array}\right.$．

点评 本题考查旋转、轴对称、一次函数等知识，利用方程组求点M坐标是解决问题的关键，必须掌握正确画出图象，学会分类讨论．