
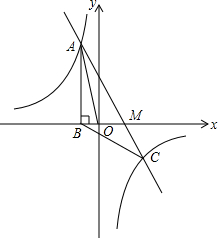
 如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(-1,4),C(m,-2),AB⊥x轴,垂足为点B.
如图,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(-1,4),C(m,-2),AB⊥x轴,垂足为点B.分析 (1)首先将点A的坐标代入反比例函数的解析式求得反比例函数的解析式,然后将点C的坐标代入求得点C的坐标,从而利用待定系数法确定一次函数是的解析式即可;
(2)根据求得的点A和点C的坐标结合函数的图象确定x的取值范围即可;
(3)分以OA为底边、以OA为腰且以A为顶点和以OA为腰且以O为顶点三种情况确定点P的坐标即可.
解答 解:(1)把点A(-1,4)代入y2=$\frac{k}{x}$中,得4=$\frac{k}{-1}$
解得k=-4,即双曲线解析式为y2=-$\frac{4}{x}$,
把点C(m,-2)代入y2=-$\frac{4}{x}$中,得-2=-$\frac{4}{m}$
解得,m=2,
∴C(2,-2),
∵一次函数y1=ax+b的图象经过A、C,
∴$\left\{\begin{array}{l}{-a+b=4}\\{2a+b=-2}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$,
所以直线解析式为y1=-2x+2;
(2)∵一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A、C两点,坐标分别为(-1,4)、(2,-2).
∴当y2>y1时,-1<x<0或x>2.
(3)如图,∵点A(-1,4),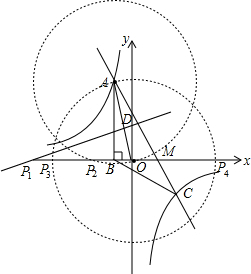
∴OA=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
当以AO为底边时,由△P1DO∽△ABO,
∴$\frac{{P}_{1}O}{AO}$=$\frac{OD}{OB}$,
即:$\frac{{P}_{1}O}{\sqrt{17}}$=$\frac{\frac{\sqrt{17}}{2}}{1}$,
解得:P1O=$\frac{17}{2}$,
∴点P1的坐标为(-$\frac{17}{2}$,0);
当以AO为腰以A为顶点时,
P2B=BO=1,
此时点P2的坐标为(-2,0);
当以AO为腰以O为顶点时,
P3O=P4O=OA=$\sqrt{17}$,
此时点P3的坐标为(-$\sqrt{17}$,0),点P4的坐标为($\sqrt{17}$,0).
点评 本题考查了反比例函数的综合知识,题目中涉及到了待定系数法确定反比例函数和一次函数的解析式及分类讨论的数学思想,知识点较多,难度较大.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | 13.22×106 | B. | 1.322×107 | C. | 1.322×103 | D. | 0.1322×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
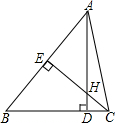 如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知∠B=48°,∠BAC=72°,求∠CAD与∠DHE的度数.
如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知∠B=48°,∠BAC=72°,求∠CAD与∠DHE的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P是⊙O外一点,A、B、C是⊙O上的三点,∠AOB=60°,PA、PB分别交$\widehat{ACB}$于M、N两点,则∠APB的范围是0°<∠APB<30°.
如图,P是⊙O外一点,A、B、C是⊙O上的三点,∠AOB=60°,PA、PB分别交$\widehat{ACB}$于M、N两点,则∠APB的范围是0°<∠APB<30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com