
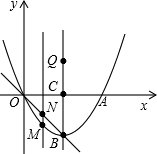
 如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).分析 (1)由题意易知,抛物线对称轴x=2,又顶点在y=-x上,得到顶点B(2,-2),用顶点坐标公式求系数a、b的值即可;
(2)列出|y0|-|x0|与x的函数关系式,求函数顶点坐标即可;
(3)能;首先求出N的坐标,然后分类讨论,BN为对角线和BN为边两种情况分析.
解答 解:(1)∵抛物线的对称轴与x轴交于点C(2,0),
∴对称轴为:x=2,
∵其顶点B在直线l:y=-x上,
∴B(2,-2)
∴$\left\{\begin{array}{l}{-\frac{b}{2a}=2}\\{\frac{-{b}^{2}}{4a}=-2}\end{array}\right.$
解得:a=$\frac{1}{2}$,b=-2,
∴抛物线的解析式为:y=$\frac{1}{2}$x2-2x;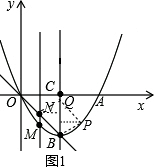
(2)∵抛物线上的点M(x0,y0)在x轴的下方,
∴x0>0,y0<0,
∴|y0|-|x0|=-($\frac{1}{2}$x2-2x)-x=-$\frac{1}{2}$x2+x=-$\frac{1}{2}$(x-1)2+$\frac{1}{2}$,
∴当x=1时,|y0|-|x0|取得最大值,
把x=1代入y=$\frac{1}{2}$x2-2x=-$\frac{3}{2}$;
∴M(1,-$\frac{3}{2}$);
(3)能;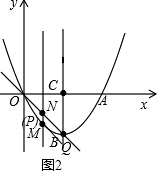
易知B(2,-2)、N(1,-1)
若以N、B、P、Q为顶点构成平行四边形,则
①如图1,当BN为对角线时,N点到对称轴的距离为1,则P到对称轴的距离等于1,则P点的横坐标为3,则P(3,-$\frac{3}{2}$);
②如图2,当BN为边时,则NP∥BQ,
∴P与M重合,
∴P(1,-$\frac{3}{2}$).
综上所述:P(3,-$\frac{3}{2}$)或P(1,-$\frac{3}{2}$).
点评 本题主要考查了待定系数法求函数关系式,二次函数图象图象与性质,二次函数最值问题,运用数形结合思想分类讨论解决平行四边形存在问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
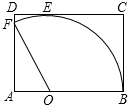 如图,从矩形ABCD中剪出一个圆心角为120°的扇形OBF,扇形OBF与CD相切,切点为E,用这个扇形围成一个圆锥.若矩形ABCD的面积为54,则围成的圆锥的高为4$\sqrt{2}$.
如图,从矩形ABCD中剪出一个圆心角为120°的扇形OBF,扇形OBF与CD相切,切点为E,用这个扇形围成一个圆锥.若矩形ABCD的面积为54,则围成的圆锥的高为4$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
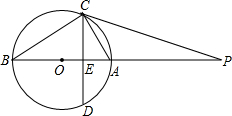 如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO
如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 4 | 2 | 2 | 1 |
| A. | 平均数是38.5 | B. | 众数是4 | C. | 中位数是40 | D. | 极差是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com