
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小亮获胜的情况,再利用概率公式即可求得答案;
(2)由小明留下剪刀手势时,可能取胜,也能不分胜负,当不会输;即可知小明应留下剪刀手势.
解答 解:(1)画树状图得: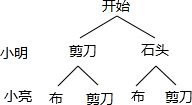
∵共有4种等可能的结果,小亮获胜的有1种情况,
∴小亮获胜的概率为$\frac{1}{4}$;
(2)小明应留下剪刀手势.
理由:∵“剪刀”胜“布”,同种手势不分胜负,
∴小明留下剪刀手势时,可能取胜,也能不分胜负,当不会输;
∵“布”胜“石头”,“石头”胜“剪刀”,
∴小明留下石头手势时,可能取胜,但也能会输;
∴小明应留下剪刀手势.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
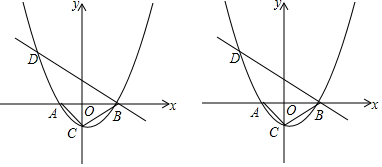
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
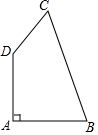 如图,在四边形ABCD中,DA⊥AB,DA=AB=$\sqrt{2}$,BC=$\sqrt{5}$,DC=1.则∠ADC的度数是135°.
如图,在四边形ABCD中,DA⊥AB,DA=AB=$\sqrt{2}$,BC=$\sqrt{5}$,DC=1.则∠ADC的度数是135°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
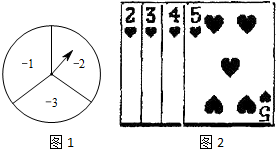 图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.
图1是一个可以自由转动的转盘,被分成了面积相等的三个扇形,分别标有数-1,-2,-3,甲转动一次转盘,转盘停止后指针指向的扇形内的数记为A(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形为止).图2背面完全一样、牌面数字分别是2,3,4,5的四张扑克牌,把四张扑克牌背面朝上,洗匀后放在桌面上,乙随机抽出一张牌面数字记为B.计算A+B的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:
篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com