
【题目】某公司生产一种成本为20元/件的新产品,在2018年1月1日投放市场,前3个月是试销售,3个月后,正常销售.
(1)试销售期间,该产品的销售价格不低于20元/件,且不能超过80元/件,销售价格![]() (元/件)与月销售量
(元/件)与月销售量![]() (万件)满足函数关系式
(万件)满足函数关系式![]() ,前3个月每件产品的定价多少元时,每月可获得最大利润?最大利润为多少?
,前3个月每件产品的定价多少元时,每月可获得最大利润?最大利润为多少?
(2)正常销售后,该种产品销售价格统一为![]() 元/件,公司每月可销售
元/件,公司每月可销售![]() 万件,从第4个月开始,每月可获得的最大利润是多少万元?
万件,从第4个月开始,每月可获得的最大利润是多少万元?
【答案】(1)80元,150万元;(2)605万元.
【解析】
(1)根据每月利润=每件产品的利润×销售量,列出利润与销售价格x的函数关系,再根据x的取值范围,即可求出每月可获得的最大利润,
(2)从第4个月开始,每月利润=每件产品的利润×销售量,列出利润与销售价格m的函数关系,再根据m的取值范围,即可求出每月可获得的最大利润.
解:(1)∵每件产品的利润为(x﹣20)元,销售量![]() (万件),
(万件),
∴每月利润(万元)![]() =200﹣
=200﹣![]() (万元),
(万元),
∵20≤x≤80,
∴当x=80时,y取得最大值,即每月利润最大,
把x=80代入得:每月利润=150万元
即最大利润为150万元;
答:前3个月每件产品的定价80元时,每月可获得最大利润,最大利润为150万元,
(2)∵每件产品的利润为(80﹣m﹣20)元,即(60﹣m)元,销售量为(10+0.2m)万件,
∴每月利润y=(60﹣m)×(10+0.2m),
整理后得:每月利润y=﹣0.2m2+2m+600=﹣0.2(m﹣5)2+605,
∵a= -0.2<0,每件产品的利润(60﹣m)≥0,即m≤60,
∴当m=5时,每月最大利润为605万元,
答:从第4个月开始,每月可获得的最大利润是605万元.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
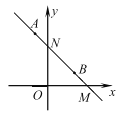
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
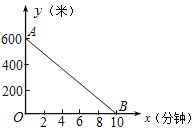
【题目】小明、小军是同班同学.某日,两人放学后去体育中心游泳,小明16:00从学校出发,小军16:03也从学校出发,沿相同的路线追赶小明.设小明出发x分钟后,与体育中心的距离为y米.如图,线段AB表示y与x之间的函数关系.
(1)求y与x之间的函数解析式;(不要求写出定义域)
(2)如果小军的速度是小明的1.5倍,那么小军用了多少分钟追上小明?此时他们距离体育中心多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数k使关于x的不等式组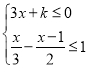 只有4个整数解,且使关于y的分式方程
只有4个整数解,且使关于y的分式方程![]() +1=
+1=![]() 的解为正数,则符合条件的所有整数k的积为( )
的解为正数,则符合条件的所有整数k的积为( )
A.2B.0C.﹣3D.﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字﹣1,﹣2和2.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=﹣x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
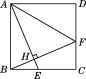
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com