
分析 直接利用提取公因式法分解因式,进而再利用平方差公式分解因式,利用不等式组的解法分别解不等式求出即可.
解答 解:ax2-ay2=a(x2-y2)=a(x+y)(x-y);
$\left\{\begin{array}{l}{3x≥-6①}\\{x-3≤0②}\end{array}\right.$,
解①得:x≥-2,
解②得:x≤3,
∴等式组$\left\{{\begin{array}{l}{3x≥-6}\\{x-3≤0}\end{array}}\right.$的解集是:-2≤x≤3.
故答案为:a(x+y)(x-y);-2≤x≤3.
点评 此题主要考查了提取公因式法以及公式法分解因式以及一元一次不等式组的解法,正确解不等式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
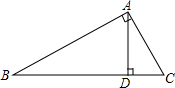 如图所示,下列说法不正确的是( )
如图所示,下列说法不正确的是( )| A. | 点B到AC的垂线段是线段AB | B. | 点C到AB的垂线段是线段AC | ||
| C. | 线段AD是点D到AB的垂线段 | D. | 线段BD是点B到AD的垂线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com