
【题目】某企业接到一批产品的生产任务,按要求必须在20天内完成,已知每件产品的售价为65元,工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=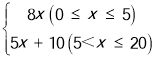 .
.
(1)工人甲第几天生产的产品数量为100件?
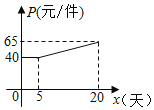
(2)设第x天(0≤x≤20)生产的产品成本为P元/件,P与x的函数图象如图,工人甲第x天创造的利润为W元.
①求P与x的函数关系式;
②求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
【答案】(1)18;(2)①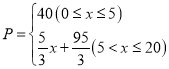 ;②第9天时,利润最大,最大利润是1008
;②第9天时,利润最大,最大利润是1008![]() 元
元
【解析】
(1)将100代入原关系式分别求出各自情况下的x的值,由此进一步根据题意分析判断即可;
(2)①根据函数图像分![]() 以及
以及![]() 两种情况,并且当
两种情况,并且当![]() 时利用待定系数法求出解析式即可;②同样,根据题意分
时利用待定系数法求出解析式即可;②同样,根据题意分![]() 以及
以及![]() 两种情况得出各自情况下的函数关系式,最后根据关系式进一步分析即可.
两种情况得出各自情况下的函数关系式,最后根据关系式进一步分析即可.
(1)当![]() 时,
时,![]() ,则令8x=100,得x=12.5(舍去),
,则令8x=100,得x=12.5(舍去),
当![]() 时,
时,![]() ,则令5x+10=100,得x=18,
,则令5x+10=100,得x=18,
答:工人甲第18天生产的产品数量为100件;
(2)①由图象可得,
当![]() 时,P=40,
时,P=40,
当![]() 时,设P与x的函数关系式为P=kx+b,
时,设P与x的函数关系式为P=kx+b,
由图象可得:![]() ,
,
解得: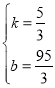 ,
,
即当![]() 时,P与x的函数关系式为P=
时,P与x的函数关系式为P=![]() x+
x+![]() ,
,
由上可得,P与x的函数关系式为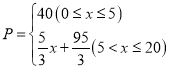 ;
;
②当![]() 时,
时,![]() ,
,
故当x=5时,W取得最大值,此时W=1000;
当![]() 时,
时,![]() ,
,
∴当x=9时,W取得最大值,此时W=1008![]() ,
,
由上可得,W与x的函数关系式是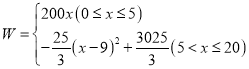 ,
,
答:第9天时,利润最大,最大利润是1008![]() 元.
元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点A在
,点A在![]() 上,四边形
上,四边形![]() 是矩形,连接
是矩形,连接![]() 、
、![]() 交于点E,连接
交于点E,连接![]() 交
交![]() 于点F.下列4个判断:①
于点F.下列4个判断:①![]() 平分
平分![]() ;②
;②![]() ;③
;③![]() ;④若点G是线段
;④若点G是线段![]() 的中点,则
的中点,则![]() 为等腰直角三角形.正确判断的个数是( )
为等腰直角三角形.正确判断的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
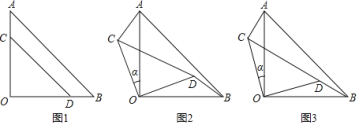
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=13,CD=7.保持纸片AOB不动,将纸片COD绕点O逆时针旋转a(0![]() α
α![]() 90°),如图2所示.当BD与CD在同一直线上(如图3)时,则△ABC的面积为____.
90°),如图2所示.当BD与CD在同一直线上(如图3)时,则△ABC的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
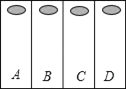
【题目】如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关.
(1)求王老师按下第一个开关恰好能打开第一排日光灯的概率;
(2)王老师按下两个开关恰好能打开第一排与第三排日光灯的概率是多少?请列表格或画树状图加以分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
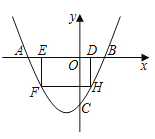
【题目】如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B,与y轴交于点C,且OC=2OB,点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH,点H、F在抛物线上,点E在x轴上.
(1)求抛物线的解析式;
(2)当矩形DEFH的周长最大时,求矩形DEFH的面积;
(3)在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N.若MN恰好平分矩形DEFH的面积,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
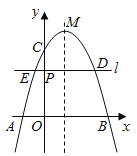
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() (点
(点![]() 位于对称轴的左侧),与
位于对称轴的左侧),与![]() 轴交于点
轴交于点![]() .已知
.已知![]() .
.
![]() 求该二次函数的对称轴及点
求该二次函数的对称轴及点![]() 的坐标.
的坐标.
![]() 点
点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() 轴交图象于点
轴交图象于点![]() (点
(点![]() 在点
在点![]() 的左侧),将顶点
的左侧),将顶点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,若点
,若点![]() 在
在![]() 轴上方,且到
轴上方,且到![]() 轴距离为1,求
轴距离为1,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[m﹣1,m+1,﹣2m]的函数的一些结论,其中不正确的是( )
A.当m=2时,函数图象的顶点坐标为![]()
B.当m>1时,函数图象截x轴所得的线段长大于3
C.当m<0时,函数在x<![]() 时,y随x的增大而增大
时,y随x的增大而增大
D.不论m取何值,函数图象经过两个定点
查看答案和解析>>
科目:初中数学 来源: 题型:
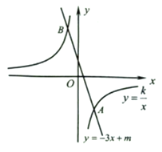
【题目】如图,直线![]() 向上平移2个单位,得到直线
向上平移2个单位,得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 的一个交点
的一个交点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)直线![]() 与双曲线
与双曲线![]() 的另一个交点为
的另一个交点为![]() ,求坐标原点
,求坐标原点![]() 到线段
到线段![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com