
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[m﹣1,m+1,﹣2m]的函数的一些结论,其中不正确的是( )
A.当m=2时,函数图象的顶点坐标为![]()
B.当m>1时,函数图象截x轴所得的线段长大于3
C.当m<0时,函数在x<![]() 时,y随x的增大而增大
时,y随x的增大而增大
D.不论m取何值,函数图象经过两个定点
【答案】C
【解析】
A、把m=2代入[m﹣1,1+m,﹣2m],求得[a,b,c],求得解析式,利用顶点坐标公式解答即可;
B、首先求得对称轴,利用二次函数的性质解答即可;
C、当x大于二分之一时,在对称轴右侧,又开口向下,所以y随x增大而减小正确;
D、根据特征数的特点,直接得出x的值,进一步验证即可解答.
因为函数y=ax2+bx+c的特征数为[m﹣1,m+1,﹣2m];
A、当m=2时,y=x2+3x﹣4=(x+![]() )2﹣
)2﹣![]() ,顶点坐标是(﹣
,顶点坐标是(﹣![]() ,﹣
,﹣![]() );此结论正确;
);此结论正确;
B、当m>1时,令y=0,有(m﹣1)x2+(1+m)x﹣2m=0,解得,x1=﹣1,x2=![]() ,
,
|x2﹣x1|=![]() >3,所以当m>1时,函数图象截x轴所得的线段长度大于3,此结论正确;
>3,所以当m>1时,函数图象截x轴所得的线段长度大于3,此结论正确;
C、当m<0时,y=(m﹣1)x2+(1+m)x﹣2m 是一个开口向下的抛物线,其对称轴是:x=﹣![]() ,在对称轴的左边y随x的增大而增大,
,在对称轴的左边y随x的增大而增大,
因为当m<0时,﹣![]() =﹣
=﹣![]() =﹣
=﹣![]() ﹣
﹣![]() >﹣
>﹣![]() ,即对称轴在x=﹣
,即对称轴在x=﹣![]() 右边,可能大于
右边,可能大于![]() ,所以在x>
,所以在x>![]() 时,y随x的增大而减小,此结论错误;
时,y随x的增大而减小,此结论错误;
D、当x=1时,y=(m﹣1)x2+(1+m)x﹣2m=0 即对任意m,函数图象都经过点(1,0),那么同样的:当x=﹣2时,y=(m﹣1)x2+(1+m)x﹣2m=﹣6,即对任意m,函数图象都经过一个点(﹣2,﹣6),此结论正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】某企业接到一批产品的生产任务,按要求必须在20天内完成,已知每件产品的售价为65元,工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=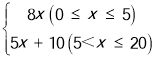 .
.
(1)工人甲第几天生产的产品数量为100件?
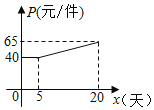
(2)设第x天(0≤x≤20)生产的产品成本为P元/件,P与x的函数图象如图,工人甲第x天创造的利润为W元.
①求P与x的函数关系式;
②求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:

(1)求y与x之间的函数关系式;
(2)若该商品的销售单价在45元~80元之间浮动,
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商场想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
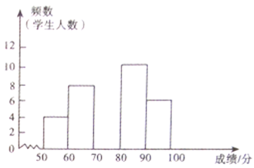
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
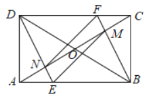
【题目】如图,矩形![]() 中,
中,![]() 相交于点O,过点B作
相交于点O,过点B作![]() 交
交![]() 于点F,交
于点F,交![]() 于点M,过点D作
于点M,过点D作![]() 交
交![]() 于点E,交
于点E,交![]() 于点N,连接
于点N,连接![]() .则下列结论:
.则下列结论:
①![]() ;②
;②![]() ;
;
③![]() ;④当
;④当![]() 时,四边形
时,四边形![]() 是菱形.
是菱形.
其中,正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
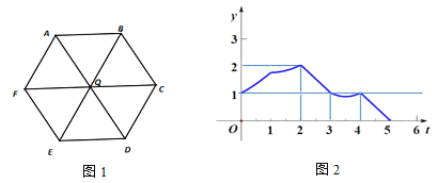
【题目】如图,点![]() 为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒
为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒![]() 个单位长度的速度在图 1 中给出的线段路径上运行,柱柱同学将机器人运行时间设为
个单位长度的速度在图 1 中给出的线段路径上运行,柱柱同学将机器人运行时间设为![]() 秒,机器人到点
秒,机器人到点![]() 距离设为
距离设为![]() ,得到函数图象如图 2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为
,得到函数图象如图 2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为![]() ;②当
;②当![]() 时,机器人一定位于点
时,机器人一定位于点![]() ;③机器人一定经过点
;③机器人一定经过点![]() ;④机器人一定经过点
;④机器人一定经过点![]() ;其中正确的有_____.
;其中正确的有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com