
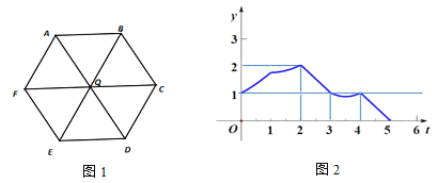
ЎѕМвДїЎїИзНјЈ¬µг![]() ОЄХэБщ±ЯРО¶ФЅЗПЯµДЅ»µгЈ¬»ъЖчИЛЦГУЪёГХэБщ±ЯРОµДДі¶Ґµгґ¦.ЦщЦщН¬С§ІЩїШ»ъЖчИЛТФГїГл
ОЄХэБщ±ЯРО¶ФЅЗПЯµДЅ»µгЈ¬»ъЖчИЛЦГУЪёГХэБщ±ЯРОµДДі¶Ґµгґ¦.ЦщЦщН¬С§ІЩїШ»ъЖчИЛТФГїГл![]() ёцµҐО»і¤¶ИµДЛЩ¶ИФЪНј 1 ЦРёшіцµДПЯ¶ОВ·ѕ¶ЙПФЛРРЈ¬ЦщЦщН¬С§Ѕ«»ъЖчИЛФЛРРК±јдЙиОЄ
ёцµҐО»і¤¶ИµДЛЩ¶ИФЪНј 1 ЦРёшіцµДПЯ¶ОВ·ѕ¶ЙПФЛРРЈ¬ЦщЦщН¬С§Ѕ«»ъЖчИЛФЛРРК±јдЙиОЄ![]() ГлЈ¬»ъЖчИЛµЅµг
ГлЈ¬»ъЖчИЛµЅµг![]() ѕаАлЙиОЄ
ѕаАлЙиОЄ![]() Ј¬µГµЅєЇКэНјПуИзНј 2.НЁ№э№ЫІмєЇКэНјПуЈ¬їЙТФµГµЅПВБРНЖ¶ПЈєўЩёГХэБщ±ЯРОµД±Яі¤ОЄ
Ј¬µГµЅєЇКэНјПуИзНј 2.НЁ№э№ЫІмєЇКэНјПуЈ¬їЙТФµГµЅПВБРНЖ¶ПЈєўЩёГХэБщ±ЯРОµД±Яі¤ОЄ![]() Ј»ўЪµ±
Ј»ўЪµ±![]() К±Ј¬»ъЖчИЛТ»¶ЁО»УЪµг
К±Ј¬»ъЖчИЛТ»¶ЁО»УЪµг![]() Ј»ўЫ»ъЖчИЛТ»¶Ёѕ№эµг
Ј»ўЫ»ъЖчИЛТ»¶Ёѕ№эµг![]() Ј»ўЬ»ъЖчИЛТ»¶Ёѕ№эµг
Ј»ўЬ»ъЖчИЛТ»¶Ёѕ№эµг![]() Ј»ЖдЦРХэИ·µДУР_____Ј®
Ј»ЖдЦРХэИ·µДУР_____Ј®
Ўѕґр°ёЎїўЩўЪўЫ
ЎѕЅвОцЎї
ёщѕЭНјПуЖрКјО»ЦГІВПлµгB»тFОЄЖрµгЈ¬ФтїЙТФЕР¶ПўЩХэИ·Ј¬ўЬґнОуЈ»ЅбєПНјПуЕР¶П![]() НјПуµД¶ФіЖРФїЙТФЕР¶ПўЪХэИ·Ј»ЅбєПНјПуТЧµГўЫХэИ·Ј»
НјПуµД¶ФіЖРФїЙТФЕР¶ПўЪХэИ·Ј»ЅбєПНјПуТЧµГўЫХэИ·Ј»
УЙНјПуїЙЦЄЈ¬»ъЖчИЛѕаАлAКЗ1ёцµҐО»і¤¶ИЈ¬їЙДЬФЪF»тBµгЈ¬ФтХэБщ±ЯРО±Яі¤ОЄ1Ј¬№КўЩХэИ·Ј»
№ЫІмНјП󣬵±![]() К±Ј¬ёщѕЭНјПуѕЯУР¶ФіЖРФїЙЦЄЈ¬»ъЖчИЛФЪOB»тOFЙПЈ¬Фтµ±t=3К±Ј¬»ъЖчИЛѕаАлµгAѕаАлОЄ1ёцµҐО»і¤¶ИЈ¬»ъЖчИЛТ»¶ЁО»УЪµгOЈ¬№КўЪХэИ·Ј»
К±Ј¬ёщѕЭНјПуѕЯУР¶ФіЖРФїЙЦЄЈ¬»ъЖчИЛФЪOB»тOFЙПЈ¬Фтµ±t=3К±Ј¬»ъЖчИЛѕаАлµгAѕаАлОЄ1ёцµҐО»і¤¶ИЈ¬»ъЖчИЛТ»¶ЁО»УЪµгOЈ¬№КўЪХэИ·Ј»
ЛщУРµгЦРЈ¬Ц»УРµгDµЅAѕаАлОЄ2ёцµҐО»Ј¬№КўЫХэИ·Ј»
ТтОЄ»ъЖчИЛїЙДЬФЪF»тBµгіц·ўЈ¬µ±ґУBіц·ўК±Ј¬І»ѕ№эµгEЈ¬№КўЬґнОуЈ»
№Кґр°ёОЄўЩўЪўЫЈ®


 ЕаУЕєГѕнµҐФЄјУЖЪД©ѕнПµБРґр°ё
ЕаУЕєГѕнµҐФЄјУЖЪД©ѕнПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї¶ЁТе[aЈ¬bЈ¬c]ОЄєЇКэy=ax2+bx+cµДМШХчКэЈ¬ПВГжёшіцМШХчКэОЄ[m©Ѓ1Ј¬m+1Ј¬©Ѓ2m]µДєЇКэµДТ»Р©ЅбВЫЈ¬ЖдЦРІ»ХэИ·µДКЗЈЁЎЎЎЎЈ©
A.µ±m=2К±Ј¬єЇКэНјПуµД¶ҐµгЧш±кОЄ![]()
B.µ±mЈѕ1К±Ј¬єЇКэНјПуЅШxЦбЛщµГµДПЯ¶Оі¤ґуУЪ3
C.µ±mЈј0К±Ј¬єЇКэФЪxЈј![]() К±Ј¬yЛжxµДФцґу¶шФцґу
К±Ј¬yЛжxµДФцґу¶шФцґу
D.І»ВЫmИЎєОЦµЈ¬єЇКэНјПуѕ№эБЅёц¶Ёµг
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬Ц±ПЯ![]() ПтЙПЖЅТЖ2ёцµҐО»Ј¬µГµЅЦ±ПЯ
ПтЙПЖЅТЖ2ёцµҐО»Ј¬µГµЅЦ±ПЯ![]() Ј¬Ц±ПЯ
Ј¬Ц±ПЯ![]() УлЛ«ЗъПЯ
УлЛ«ЗъПЯ![]() µДТ»ёцЅ»µг
µДТ»ёцЅ»µг![]() µДЧЭЧш±кОЄ
µДЧЭЧш±кОЄ![]() Ј®
Ј®
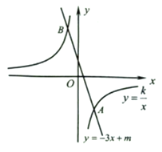
ЈЁ1Ј©Зу![]() µДЦµЈ»
µДЦµЈ»
ЈЁ2Ј©µ±![]() К±Ј¬Зу
К±Ј¬Зу![]() µДИЎЦµ·¶О§Ј»
µДИЎЦµ·¶О§Ј»
ЈЁ3Ј©Ц±ПЯ![]() УлЛ«ЗъПЯ
УлЛ«ЗъПЯ![]() µДБнТ»ёцЅ»µгОЄ
µДБнТ»ёцЅ»µгОЄ![]() Ј¬ЗуЧш±кФµг
Ј¬ЗуЧш±кФµг![]() µЅПЯ¶О
µЅПЯ¶О![]() µДѕаАлЈ®
µДѕаАлЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
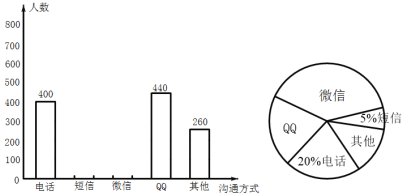
ЎѕМвДїЎїЅсДкТЯЗйЖЪјдЈ¬ОЄ·АЦ№ТЯЗйА©ЙўЈ¬ИЛГЗјыГжµД»ъ»бЙЩБЛЈ¬µ«КЗЛжЧЕНЁС¶јјКхСёГН·ўХ№Ј¬ИЛУлИЛЦ®јдµД№µНЁ·ЅКЅёь¶аСщЎў±гЅЭЈ¬ОЄґЛЈ¬ЛпАПК¦ЙијЖБЛЎ°ДгЧоПІ»¶µД№µНЁ·ЅКЅЎ±µчІйОКѕнЈЁГїИЛ±ШСЎЗТЦ»СЎТ»ЦЦЈ©ЅшРРµчІй.Ѕ«НіјЖЅб№ы»жЦЖБЛИзПВБЅ·щІ»НкХыµДНіјЖНјЈ¬ЗлЅбєПНјЦРЛщёшµДРЕПўЅвґрПВБРОКМвЈє
ЈЁ1Ј©ХвґОІОУлµчІйµД№ІУР ИЛЈ»ФЪЙИРОНіјЖНјЦРЈ¬±нКѕЎ°ОўРЕЎ±µДЙИРОФІРДЅЗµД¶ИКэОЄ Ј»ЖдЛь№µНЁ·ЅКЅЛщХјµД°Щ·Ц±ИОЄ Ј®
ЈЁ2Ј©Ѕ«МхРОНіјЖНјІ№ідНкХыЈ»
ЈЁ3Ј©Из№ыОТ№ъУР13ТЪИЛФЪК№УГКЦ»ъЈ®
ўЩЗл№АјЖЧоПІ»¶УГЎ°ОўРЕЎ±ЅшРР№µНЁµДИЛКэЈ»
ўЪФЪИ«№ъК№УГКЦ»ъµДИЛЦРЛж»ъійИЎТ»ИЛЈ¬УГЖµВК№АјЖёЕВКЈ¬ЗуійИЎµДЗЎєГК№УГЎ°QQЎ±µДёЕВККЗ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЙъ»оА¬»ш·ЦАа»ШКХКЗКµПЦА¬»шјхБї»ЇєНЧКФґ»ЇµДЦШТЄНѕѕ¶єНКЦ¶ОЈ®ОЄБЛЅв2019ДкДіКРµЪ¶юјѕ¶ИИХѕщїЙ»ШКХОп»ШКХБїЗйїцЈ¬Лж»ъійИЎёГКР2019ДкµЪ¶юјѕ¶ИµД![]() МмКэѕЭЈ¬ХыАнєу»жЦЖіЙНіјЖ±нЅшРР·ЦОцЈ®
МмКэѕЭЈ¬ХыАнєу»жЦЖіЙНіјЖ±нЅшРР·ЦОцЈ®
ИХѕщїЙ»ШКХОп»ШКХБїЈЁЗ§¶ЦЈ© |
|
|
|
|
| єПјЖ |
ЖµКэ | 1 | 2 |
| 3 |
| |
ЖµВК | 0.05 | 0.10 |
| 0.15 | 1 |
±нЦР![]() ЧйµДЖµВК
ЧйµДЖµВК![]() ВъЧг
ВъЧг![]() Ј®
Ј®
ПВГжУРЛДёцНЖ¶ПЈє
ўЩ±нЦР![]() µДЦµОЄ20Ј»
µДЦµОЄ20Ј»
ўЪ±нЦР![]() µДЦµїЙТФОЄ7Ј»
µДЦµїЙТФОЄ7Ј»
ўЫХв![]() МмµДИХѕщїЙ»ШКХОп»ШКХБїµДЦРО»КэФЪ
МмµДИХѕщїЙ»ШКХОп»ШКХБїµДЦРО»КэФЪ![]() ЧйЈ»
ЧйЈ»
ўЬХв![]() МмµДИХѕщїЙ»ШКХОп»ШКХБїµДЖЅѕщКэІ»µНУЪ3Ј®
МмµДИХѕщїЙ»ШКХОп»ШКХБїµДЖЅѕщКэІ»µНУЪ3Ј®
ЛщУРєПАнНЖ¶ПµДРтєЕКЗЈЁ Ј©
A.ўЩўЪB.ўЩўЫC.ўЪўЫўЬD.ўЩўЫўЬ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ѕШРОABCDЦРЈ¬AB=3Ј¬BC=4Ј¬¶ЇµгPґУAµгіц·ўЈ¬°ґAЎъBЎъCµД·ЅПтФЪABєНBCЙПТЖ¶ЇЈ¬јЗPA=xЈ¬µгDµЅЦ±ПЯPAµДѕаАлОЄyЈ¬Фтy№ШУЪxµДєЇКэНјПуґуЦВКЗЈЁ Ј©

A. B.
B.
C. D.
D.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
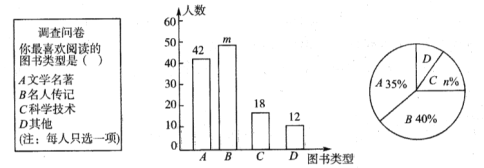
ЎѕМвДїЎїОЄБЛЕаСшС§ЙъµДФД¶БП°№ЯЈ¬ДіРЈїЄХ№БЛЎ°¶БєГКйЈ¬ЦъіЙі¤Ў±ПµБР»о¶ЇЈ¬ІўЧј±ё№єЦГТ»ЕъНјКйЈ¬№єКйЗ°Ј¬¶ФС§ЙъПІ»¶ФД¶БµДНјКйАаРНЅшРРБЛійСщµчІйЈ¬ІўЅ«µчІйКэѕЭ»жЦЖіЙБЅ·щІ»НкХыµДНіјЖНјЈ®ёщѕЭНіјЖНјЛщМṩµДРЕПўЈ¬»ШґрПВБРОКМвЈє
ЈЁ1Ј©±ѕґОµчІй№ІійІйБЛ ГыС§ЙъЈ¬НіјЖНјЦРµД![]() Ј¬
Ј¬![]() Ј®
Ј®
ЈЁ2Ј©ТСЦЄёГРЈ№ІУР960ГыС§ЙъЈ¬Зл№АјЖёГРЈПІ»¶ФД¶БЎ°![]() Ў±АаНјКйµДС§ЙъФјУР¶аЙЩИЛЈї
Ў±АаНјКйµДС§ЙъФјУР¶аЙЩИЛЈї
ЈЁ3Ј©С§РЈТЄѕЩ°м¶БКйЦЄК¶ѕєИьЈ¬ЖЯДкј¶ЈЁ1Ј©°аТЄФЪ°ај¶УЕК¤ХЯ2ДР1Е®ЦРЛж»ъСЎЛН2ИЛІОИьЈ¬ЗуСЎЛНµДБЅГыІОИьН¬С§ОЄ1ДР1Е®µДёЕВККЗ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ABКЗ°лФІOµДЦ±ѕ¶Ј¬ЗТABЈЅ6cmЈ¬µгCОЄ°лФІЙПµДТ»µгЈ¬Ѕ«ґЛ°лФІСШBCЛщФЪµДЦ±ПЯХЫµюЈ¬ИфФІ»ЎBCЗЎєГ№эФІРДOЈ¬ФтНјЦРТхУ°Ії·ЦµДГж»эКЗ_____Ј®
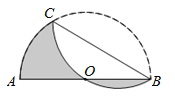
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЕЧОпПЯCЈєyЈЅax2©Ѓ2ax+3їЄїЪПтПВЈ®
ЈЁ1Ј©µ±ЕЧОпПЯC№эµгЈЁ1Ј¬4Ј©К±Ј¬ЗуaµДЦµєНЕЧОпПЯУлyЦбµДЅ»µгЧш±кЈ»
ЈЁ2Ј©Зу¶юґОєЇКэyЈЅax2©Ѓ2ax+3µД¶ФіЖЦбєНЧоґуЦµЈЁУГє¬aµДКЅЧУ±нКѕЈ©Ј»
ЈЁ3Ј©Ѕ«ЕЧОпПЯCПтЧуЖЅТЖaёцµҐО»µГµЅЕЧОпПЯC1Ј¬ЛжЧЕaµД±д»ЇЈ¬ЕЧОпПЯC1¶ҐµгµДЧЭЧш±кyУлєбЧш±кxЦ®јдґжФЪТ»ёцєЇКэ№ШПµЈ¬ЗуХвёцєЇКэ№ШПµКЅЈ¬ІўРґіцЧФ±дБїxµДИЎЦµ·¶О§Ј»
ЈЁ4Ј©јЗЈЁ3Ј©ЛщЗуµДєЇКэОЄDЈ¬ЕЧОпПЯCУлєЇКэDµДНјПуЅ»УЪµгMЈ¬ЅбєПНјПуЈ¬ЗлЦ±ЅУРґіцµгMµДЧЭЧш±кµДИЎЦµ·¶О§Ј®
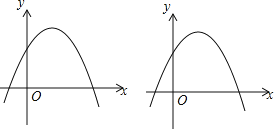
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com