
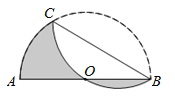
【题目】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:
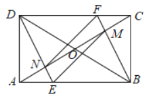
【题目】如图,矩形![]() 中,
中,![]() 相交于点O,过点B作
相交于点O,过点B作![]() 交
交![]() 于点F,交
于点F,交![]() 于点M,过点D作
于点M,过点D作![]() 交
交![]() 于点E,交
于点E,交![]() 于点N,连接
于点N,连接![]() .则下列结论:
.则下列结论:
①![]() ;②
;②![]() ;
;
③![]() ;④当
;④当![]() 时,四边形
时,四边形![]() 是菱形.
是菱形.
其中,正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
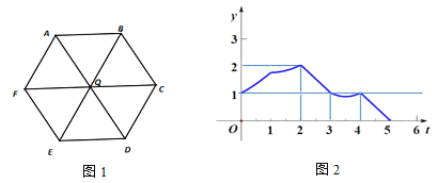
【题目】如图,点![]() 为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒
为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒![]() 个单位长度的速度在图 1 中给出的线段路径上运行,柱柱同学将机器人运行时间设为
个单位长度的速度在图 1 中给出的线段路径上运行,柱柱同学将机器人运行时间设为![]() 秒,机器人到点
秒,机器人到点![]() 距离设为
距离设为![]() ,得到函数图象如图 2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为
,得到函数图象如图 2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为![]() ;②当
;②当![]() 时,机器人一定位于点
时,机器人一定位于点![]() ;③机器人一定经过点
;③机器人一定经过点![]() ;④机器人一定经过点
;④机器人一定经过点![]() ;其中正确的有_____.
;其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
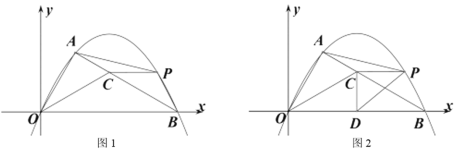
【题目】如图 ![]() ,在平面直角坐标系中,
,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在第一象限,
在第一象限,![]() 在
在![]() 轴上, 且
轴上, 且![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线.抛物线
的角平分线.抛物线![]() 过点
过点![]() ,
,![]() ,点
,点 ![]() 在直线
在直线![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() ,
,![]() ,
,![]() .
.
(1)填空:抛物线解析式为 ,直线![]() 解析式为 ;
解析式为 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)如图![]() ,作
,作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边上一点(不与端点重合),将
边上一点(不与端点重合),将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
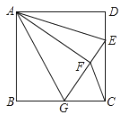
①![]() __________;
__________;
②若![]() 为
为![]() 的中点,则
的中点,则![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
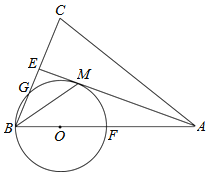
【题目】如图,在![]() ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)若BC=8,AC=12时,求⊙O的半径和线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是__________.(填“方案一”、“方案二”或“方案三”)
(2)学校根据样本数据,绘制成下表(90分及以上为“优秀”,60分及以上为“及格”):
样本容量 | 平均分 | 及格率 | 优秀率 | 最高分 | 最低分 |
100 | 93.5 |
|
| 100 | 80 |
分数段统计(学生成绩记为 | |||||
分数段 |
|
|
|
|
|
频数 | 0 | 5 | 25 | 30 | 40 |
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到“优秀”的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则△PMN周长的最小值是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com