
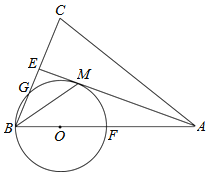
【题目】如图,在![]() ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)若BC=8,AC=12时,求⊙O的半径和线段BG的长.
【答案】(1)证明见解析;(2)半径为3,BG=2
【解析】
(1)连接OM,由AB=AC、AE平分∠BAC,得到AE⊥BC;利用角平分线的性质和等腰三角形的性质,得到OM∥BC;再利用平行线的性质得到AE⊥OM,即可证得AE为⊙O的切线.
(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用相似三角形的性质得到![]() ,即
,即![]() ,解得R=3,从而求得⊙O的半径;过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
,解得R=3,从而求得⊙O的半径;过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
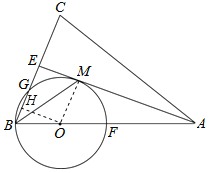
(1)证明:如图,连接OM,
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC,
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)解:设⊙O的半径为R,
∵BC=8,
∴BE=![]() BC=4,
BC=4,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() ,
,
即![]() ,
,
解得:R=3,
∴⊙O的半径为3;
如图,过点O作OH⊥BG于点H,
则BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=BE-HE=![]() BC - HE =4-3=1,
BC - HE =4-3=1,
∴BG=2BH=2.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
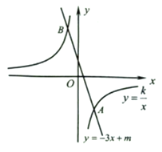
【题目】如图,直线![]() 向上平移2个单位,得到直线
向上平移2个单位,得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 的一个交点
的一个交点![]() 的纵坐标为
的纵坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)直线![]() 与双曲线
与双曲线![]() 的另一个交点为
的另一个交点为![]() ,求坐标原点
,求坐标原点![]() 到线段
到线段![]() 的距离.
的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
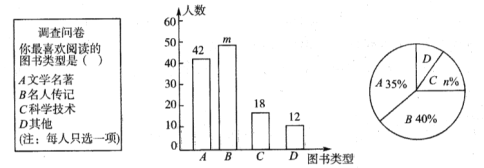
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图.根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,统计图中的![]() ,
,![]() .
.
(2)已知该校共有960名学生,请估计该校喜欢阅读“![]() ”类图书的学生约有多少人?
”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年级(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛同学为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
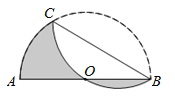
【题目】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
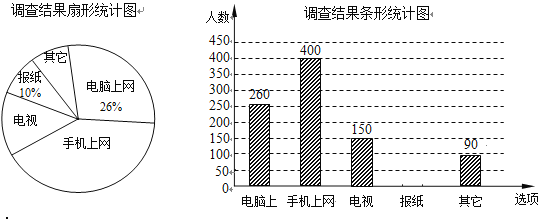
根据以上信息解答下列问题:
(1)这次抽样调查的样本容量是 ;
(2)通过“电视”了解新闻的人数占被调查人数的百分比为 ;扇形统计图中, “手机上网”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有70万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解一批电池的使用寿命,应采用全面调查的方式
B.数据![]() ,
,![]() ,...,
,...,![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,则数据
,则数据![]() ,
,![]() ,...,
,...,![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]()
C.通过对甲、乙两组学生数学成绩的跟踪调查,整理计算得到甲、乙两组数据的方差为![]() ,
,![]() ,则乙数据较为稳定
,则乙数据较为稳定
D.为了解官渡区九年级![]() 多名学生的视力情况,从中随机选取
多名学生的视力情况,从中随机选取![]() 名学生的视力情况进行分析,则选取的样本容量为
名学生的视力情况进行分析,则选取的样本容量为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=ax2﹣2ax+3开口向下.
(1)当抛物线C过点(1,4)时,求a的值和抛物线与y轴的交点坐标;
(2)求二次函数y=ax2﹣2ax+3的对称轴和最大值(用含a的式子表示);
(3)将抛物线C向左平移a个单位得到抛物线C1,随着a的变化,抛物线C1顶点的纵坐标y与横坐标x之间存在一个函数关系,求这个函数关系式,并写出自变量x的取值范围;
(4)记(3)所求的函数为D,抛物线C与函数D的图象交于点M,结合图象,请直接写出点M的纵坐标的取值范围.
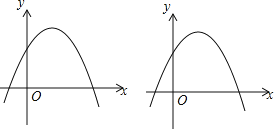
查看答案和解析>>
科目:初中数学 来源: 题型:
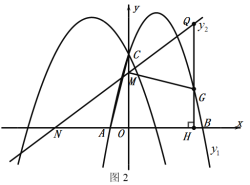
【题目】如图1,抛物线![]() 与抛物线
与抛物线![]() 相交y轴于点C,抛物线
相交y轴于点C,抛物线![]() 与x轴交于A、B两点(点B在点A的右侧),直线
与x轴交于A、B两点(点B在点A的右侧),直线![]() 交x轴负半轴于点N,交y轴于点M,且
交x轴负半轴于点N,交y轴于点M,且![]() .
.
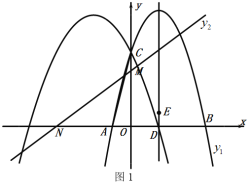
(1)求抛物线![]() 的解析式与k的值;
的解析式与k的值;
(2)抛物线![]() 的对称轴交x轴于点D,连接
的对称轴交x轴于点D,连接![]() ,在x轴上方的对称轴上找一点E,使以点A,D,E为顶点的三角形与
,在x轴上方的对称轴上找一点E,使以点A,D,E为顶点的三角形与![]() 相似,求出
相似,求出![]() 的长;
的长;
(3)如图2,过抛物线![]() 上的动点G作
上的动点G作![]() 轴于点H,交直线
轴于点H,交直线![]() 于点Q,若点
于点Q,若点![]() 是点Q关于直线
是点Q关于直线![]() 的对称点,是否存在点G(不与点C重合),使点
的对称点,是否存在点G(不与点C重合),使点![]() 落在y轴上?若存在,请直接写出点G的横坐标,若不存在,请说明理由.
落在y轴上?若存在,请直接写出点G的横坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com