
【题目】如图,直线![]() 向上平移2个单位,得到直线
向上平移2个单位,得到直线![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 的一个交点
的一个交点![]() 的纵坐标为
的纵坐标为![]() .
.
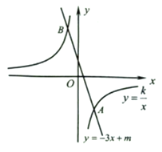
(1)求![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)直线![]() 与双曲线
与双曲线![]() 的另一个交点为
的另一个交点为![]() ,求坐标原点
,求坐标原点![]() 到线段
到线段![]() 的距离.
的距离.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据平移的原则得出m的值,并计算点A的坐标,因为A在反比例函数的图象上,代入可以求k的值;
(2)画出两函数图象,根据交点坐标写出解集;
(3)求得直线与坐标轴的交点坐标,利用面积法即可求解.
(1)∵![]() 向上平移2个单位得到:
向上平移2个单位得到:
![]() ,
,
∴![]() ,
,
∵![]() 过点
过点![]() ,且点
,且点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴A的坐标为(1,-2),
把![]() 代入
代入![]() ,得:
,得:![]() ;
;
(2)由直线![]() 与双曲线
与双曲线![]() 相交,
相交,
得:![]() ,
,
解之得:![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以交点A的坐标为(1,-2),B的坐标为(![]() ,3),
,3),
结合图像可得:当![]() 或
或![]() 时直线
时直线![]() 在双曲线
在双曲线![]() 的下方,
的下方,
∴当![]() 时,求
时,求![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ;
;
(3)直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点C、D,
轴交于点C、D,
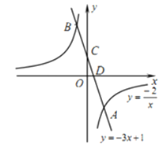
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
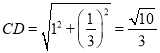 ,
,
∴点![]() 到线段
到线段![]() 的距离:
的距离:![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
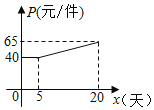
【题目】某企业接到一批产品的生产任务,按要求必须在20天内完成,已知每件产品的售价为65元,工人甲第x天生产的产品数量为y件,y与x满足如下关系:y=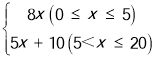 .
.
(1)工人甲第几天生产的产品数量为100件?
(2)设第x天(0≤x≤20)生产的产品成本为P元/件,P与x的函数图象如图,工人甲第x天创造的利润为W元.
①求P与x的函数关系式;
②求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
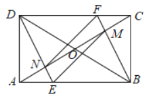
【题目】如图,矩形![]() 中,
中,![]() 相交于点O,过点B作
相交于点O,过点B作![]() 交
交![]() 于点F,交
于点F,交![]() 于点M,过点D作
于点M,过点D作![]() 交
交![]() 于点E,交
于点E,交![]() 于点N,连接
于点N,连接![]() .则下列结论:
.则下列结论:
①![]() ;②
;②![]() ;
;
③![]() ;④当
;④当![]() 时,四边形
时,四边形![]() 是菱形.
是菱形.
其中,正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 和
和![]() 均为等腰三角形,且
均为等腰三角形,且![]() .
.
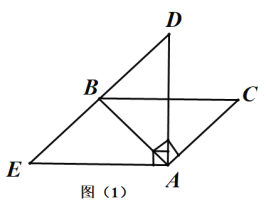
(1)如图(1),点B是![]() 的中点,判定四边形
的中点,判定四边形![]() 的形状,并说明理由;
的形状,并说明理由;
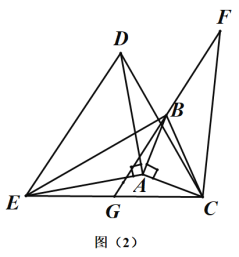
(2)如图(2),若点G是![]() 的中点,连接
的中点,连接![]() 并延长至点F,使
并延长至点F,使![]() .求证:①
.求证:①![]() ,②
,②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
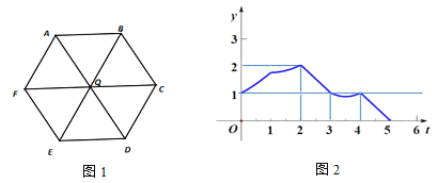
【题目】如图,点![]() 为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒
为正六边形对角线的交点,机器人置于该正六边形的某顶点处.柱柱同学操控机器人以每秒![]() 个单位长度的速度在图 1 中给出的线段路径上运行,柱柱同学将机器人运行时间设为
个单位长度的速度在图 1 中给出的线段路径上运行,柱柱同学将机器人运行时间设为![]() 秒,机器人到点
秒,机器人到点![]() 距离设为
距离设为![]() ,得到函数图象如图 2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为
,得到函数图象如图 2.通过观察函数图象,可以得到下列推断:①该正六边形的边长为![]() ;②当
;②当![]() 时,机器人一定位于点
时,机器人一定位于点![]() ;③机器人一定经过点
;③机器人一定经过点![]() ;④机器人一定经过点
;④机器人一定经过点![]() ;其中正确的有_____.
;其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
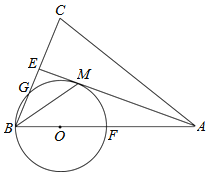
【题目】如图,在![]() ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)若BC=8,AC=12时,求⊙O的半径和线段BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com