
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,连结
的切线,连结![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() .
.
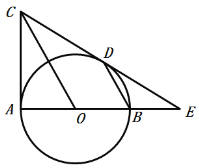
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)CD=12.
【解析】
(1)连接OD,根据切线的性质可得到∠OAC=90°,通过分析证明△CDO≌△CAO,可得OD⊥CE,即可得到结果;
(2)在Rt△ODE中,根据勾股定理可得圆的半径,根据平行线成比例得![]() ,即可得到结果;
,即可得到结果;
(1)证明:连接OD,
∵AC为⊙O的切线,
∴AC⊥AB.
∴∠OAC=90°.
∵BD∥OC,
∴∠OBD=∠AOC,∠ODB=∠COD.
∵OB、OD为⊙O的半径,
∴OB=OD.
∴∠OBD=∠ODB.
∴∠AOC=∠DOC.
在△CDO和△CAO中,
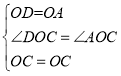
∴△CDO≌△CAO(SAS)
∴∠CDO=∠CAO=90°.
∴OD⊥CE于D,且OD是半径,
∴CE是⊙O的切线.
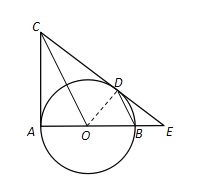
(2)解:在Rt△ODE中,∠ODE=90°,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵BD∥OC,
∴![]() ,
,
又BE=4,DE=8,BO=![]() ,
,
∴![]() ,
,
∴![]() 2.
2.


科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 为
为![]() 边上一点(不与端点重合),将
边上一点(不与端点重合),将![]() 沿
沿![]() 对折至
对折至![]() ,延长
,延长![]() 交边
交边![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
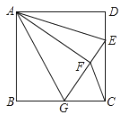
①![]() __________;
__________;
②若![]() 为
为![]() 的中点,则
的中点,则![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
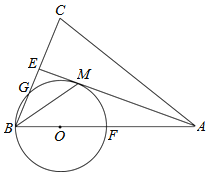
【题目】如图,在![]() ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
(1)求证:AE为⊙O的切线.
(2)若BC=8,AC=12时,求⊙O的半径和线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合理饮食对学生的身体、智力发育和健康起到了极其重要的作用,只有荤食和素食的合理搭配,才能强化初中生的身体素质,某校为了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:
从七、八年级两个年级中各抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:![]()
八年级:![]()
整理数据:
年级 |
|
|
|
|
七年级 |
|
|
|
|
八年级 |
|
|
|
|
(说明:![]() 为优秀,
为优秀,![]() 为良好,
为良好,![]() 为及格,
为及格,![]() 为不及格)
为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ,
,
(2)比较这两组样本数据的平均数、中位数和众数,你认为哪个年级的体质健康成绩比较好?请说明理由
(3)若七年级共有![]() 名学生,请估计七年级体质健康成绩优秀的学生人数
名学生,请估计七年级体质健康成绩优秀的学生人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生垃圾分类意识,推动垃圾分类进校园.某初中学校组织全校1200名学生参加了“垃圾分类知识竞赛”,为了解学生的答题情况,学校考虑采用简单随机抽样的方法抽取部分学生的成绩进行调查分析.
(1)学校设计了以下三种抽样调查方案:
方案一:从初一、初二、初三年级中指定部分学生成绩作为样本进行调查分析;
方案二:从初一、初二年级中随机抽取部分男生成绩及在初三年级中随机抽取部分女生成绩进行调查分析;
方案三:从三个年级全体学生中随机抽取部分学生成绩进行调查分析.
其中抽取的样本具有代表性的方案是__________.(填“方案一”、“方案二”或“方案三”)
(2)学校根据样本数据,绘制成下表(90分及以上为“优秀”,60分及以上为“及格”):
样本容量 | 平均分 | 及格率 | 优秀率 | 最高分 | 最低分 |
100 | 93.5 |
|
| 100 | 80 |
分数段统计(学生成绩记为 | |||||
分数段 |
|
|
|
|
|
频数 | 0 | 5 | 25 | 30 | 40 |
请结合表中信息解答下列问题:
①估计该校1200名学生竞赛成绩的中位数落在哪个分数段内;
②估计该校1200名学生中达到“优秀”的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
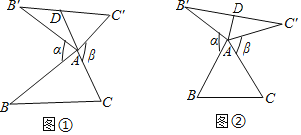
【题目】如图①,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB′C′是△ABC的旋补三角形,△AB′C′边B′C′上的中线AD叫做△ABC的旋补中线.
如图②,当△ABC为等边三角形时,△AB′C′是△ABC的旋补三角形,AD是旋补中线,AD与BC的数量关系为:AD=_____BC;当BC=8时,则B′C′长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,E为BC的中点.将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则△CDF的面积为( )
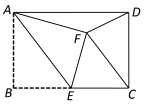
A. 3.6 B. 4.32 C. 5.4 D. 5.76
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题解答]
两个城镇![]() 与一条公路
与一条公路![]() 位置如图①所示.现电信部门需在公路
位置如图①所示.现电信部门需在公路![]() 上修建一座信号发射塔
上修建一座信号发射塔![]() 要求发射塔
要求发射塔![]() 到两个城镇
到两个城镇![]() 与
与![]() 的距离之和最短.
的距离之和最短.
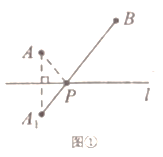
解:点![]() 作关于直线
作关于直线![]() 的对称点
的对称点![]() 连结
连结![]() ,
,
与直线![]() 的交点即为所求的点
的交点即为所求的点![]() .
.
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
![]() 直线
直线![]() 垂直平分
垂直平分![]()
![]()
![]()
![]() 点
点![]() 即为所求的点。(两点之间线段最短)
即为所求的点。(两点之间线段最短)
请根据以上问题解答,完成下列问题.
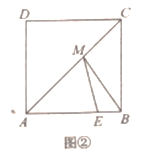
[方法运用]如图②,在正方形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,点
上,点![]() 在对角线AC上,
在对角线AC上,
(1)当点![]() 是边
是边![]() 的中点时,则
的中点时,则![]() 的最小值为 ;
的最小值为 ;
(2)若![]() 求
求![]() 周长的最小值.
周长的最小值.
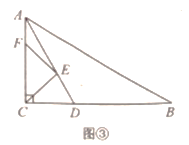
[拓展提升]如图③,在![]() 中,
中,![]() ,AD平分
,AD平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 分别在
分别在![]() 上,则
上,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com