
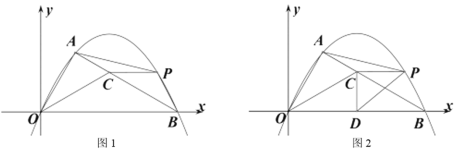
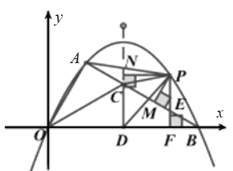
【题目】如图 ![]() ,在平面直角坐标系中,
,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在第一象限,
在第一象限,![]() 在
在![]() 轴上, 且
轴上, 且![]() ,
,![]() ,
,![]() 是
是![]() 的角平分线.抛物线
的角平分线.抛物线![]() 过点
过点![]() ,
,![]() ,点
,点 ![]() 在直线
在直线![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() ,
,![]() ,
,![]() .
.
(1)填空:抛物线解析式为 ,直线![]() 解析式为 ;
解析式为 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)如图![]() ,作
,作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标
的坐标
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)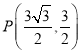
【解析】
(1)先根据直角三角形的性质求出A点坐标,把A、B两点坐标代入解析式![]() ,求得a、b的值即可;设直线AB的解析式为y=kx+c,将A、B两点坐标代入解析式y=kx+c,求出k、c的值即可.
,求得a、b的值即可;设直线AB的解析式为y=kx+c,将A、B两点坐标代入解析式y=kx+c,求出k、c的值即可.
(2)根据直角三角形的性质可知AB=3,AC=1,再根据相似三角形的判定和性质求出PA 的值,然后求出![]() 的值;
的值;
(3)作![]() 轴于
轴于![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,根据角平分线的性质得到AC=CD,由
,根据角平分线的性质得到AC=CD,由![]() 与
与![]() 的面积相等,推出PM=PN,设
的面积相等,推出PM=PN,设![]() ,则
,则![]() ,根据三角函数用含t的代数式表示PN、PM,并列出方程,求得t 的值,进而求得t的坐标.
,根据三角函数用含t的代数式表示PN、PM,并列出方程,求得t 的值,进而求得t的坐标.
解:(1)∵![]() ,
,![]() ,
,![]() ,
,
∴B(![]() ,0),A
,0),A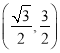
将B(![]() ,0),A
,0),A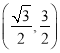 代入
代入![]() ,得
,得
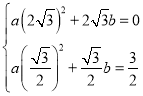
解得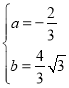
抛物线:![]()
设直线AB的解析式为:y=kx+c,
将B(![]() ,0),A
,0),A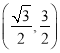 代入y=kx+c,
代入y=kx+c,
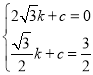
解得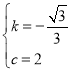
直线![]() :
:![]()
(2)在![]() 中,
中,![]() ,
,![]()
![]() ,
,![]()
![]() 平分
平分![]()
即![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
即![]()
![]()
(3)作![]() 轴于
轴于![]() 交
交![]() 于
于![]()
作![]() 于
于![]() ,
,![]() 于
于![]()
![]() 平分
平分![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
![]()
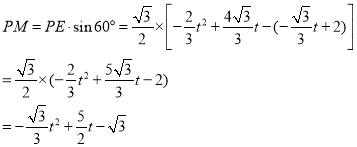
由![]() ,代入解得
,代入解得![]() (舍去),
(舍去),![]()
![]() 点
点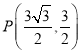


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2x+c与x轴交于点A(1,0),点B(﹣3,0),与y轴交于点C,连接BC,点P在第二象限的抛物线上,连接PC、PO,线段PO交线段BC于点 E.
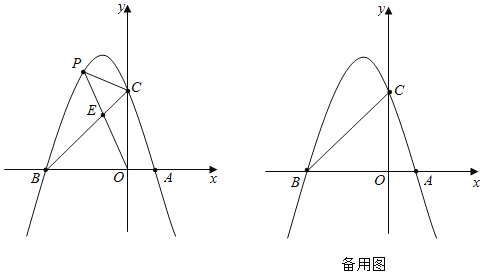
(1)求抛物线的表达式;
(2)若△PCE的面积为S1,△OCE的面积为S2,当![]() =
=![]() 时,求点P的坐标;
时,求点P的坐标;
(3)已知点C关于抛物线对称轴的对称点为点N,连接BN,点H在x轴上,当∠HCB=∠NBC时,
①求满足条件的所有点H的坐标;
②当点H在线段AB上时,点Q是线段BH外一点,QH=1,连接BQ,将线段BQ绕着点Q顺时针旋转90°,得到线段QM,连接MH,直接写出线段MH的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情期间,为防止疫情扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷,为此,孙老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种)进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有 人;在扇形统计图中,表示“微信”的扇形圆心角的度数为 ;其它沟通方式所占的百分比为 .
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.
①请估计最喜欢用“微信”进行沟通的人数;
②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?
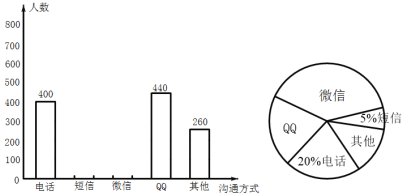
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图.根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,统计图中的![]() ,
,![]() .
.
(2)已知该校共有960名学生,请估计该校喜欢阅读“![]() ”类图书的学生约有多少人?
”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年级(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛同学为1男1女的概率是多少?
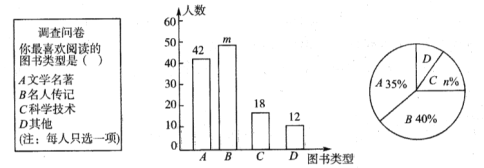
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
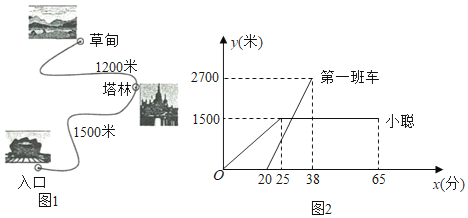
(1)求第一班车离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从人口处到达塔林所蓄的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聘聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,且AB=6cm,点C为半圆上的一点,将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是_____.
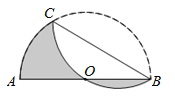
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解一批电池的使用寿命,应采用全面调查的方式
B.数据![]() ,
,![]() ,...,
,...,![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,则数据
,则数据![]() ,
,![]() ,...,
,...,![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]()
C.通过对甲、乙两组学生数学成绩的跟踪调查,整理计算得到甲、乙两组数据的方差为![]() ,
,![]() ,则乙数据较为稳定
,则乙数据较为稳定
D.为了解官渡区九年级![]() 多名学生的视力情况,从中随机选取
多名学生的视力情况,从中随机选取![]() 名学生的视力情况进行分析,则选取的样本容量为
名学生的视力情况进行分析,则选取的样本容量为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD为直径的⊙O与BC相切于点E,交CD于点F,连接DE.
(1)证明:DE平分∠ADC;
(2)已知AD=4,设CD的长为x(2<x<4).
①当x=2.5时,求弦DE的长度;
②当x为何值时,DFFC的值最大?最大值是多少?
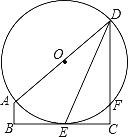
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com