
【题目】如图,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD为直径的⊙O与BC相切于点E,交CD于点F,连接DE.
(1)证明:DE平分∠ADC;
(2)已知AD=4,设CD的长为x(2<x<4).
①当x=2.5时,求弦DE的长度;
②当x为何值时,DFFC的值最大?最大值是多少?
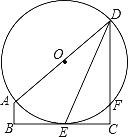
【答案】(1)见解析;(2)①![]() ;②x=3时,DFCF的值最大,最大值为2
;②x=3时,DFCF的值最大,最大值为2
【解析】
(1)连接OE,根据已知可推出AB∥OE∥CD,可得∠OED=∠CDE,再根据OD=OE,可得∠OED=∠ODE,即可证明;
(2)①连接AF交OE于H,由现有条件可推出AB=1.5,然后可证四边形ABCF是矩形,可得AH=FH,AB=CF=HE=1.5,OH=OE﹣EH=0.5,可得AH=![]() =
=![]() =
=![]() ,根据勾股定理即可得出答案;
,根据勾股定理即可得出答案;
②设AB=CF=m,根据OE=![]() (AB+CD),可得x+m=4,即可得DFCF的函数表达式,根据函数的性质即可得出答案.
(AB+CD),可得x+m=4,即可得DFCF的函数表达式,根据函数的性质即可得出答案.
(1)证明:如图,连接OE,
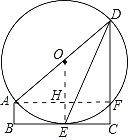
∵BC是⊙O的切线,
∴OE⊥BC,
∵AB∥CD,∠C=90°,
∴∠B=90°,
∴AB⊥BC,CD⊥BC,
∴AB∥OE∥CD,
∴∠OED=∠CDE,
∵OD=OE,
∴∠OED=∠ODE,
∴∠ODE=∠CDE,
∴ED平分∠ADC;
(2)①连接AF交OE于H,
∵AB∥OE∥CD,AO=OD,
∴BE=EC,
∴OE=![]() (AB+CD),
(AB+CD),
∵OE=2,CD=2.5,
∴AB=1.5,
∵AD是⊙O的直径,
∴∠AFD=90°,
∵∠B=∠C=9°,
∴四边形ABCF是矩形,
∴AF∥BC,
∵OE⊥BC,
∴OE⊥AF,
∴AH=FH,AB=CF=HE=1.5,
∴OH=OE﹣EH=0.5,
∴AH=![]() =
=![]() =
=![]() ,
,
∴AH=FH=CE=![]() ,
,
∴DE=![]() =
= =
=![]() ;
;
②设AB=CF=m,
∵OE=![]() (AB+CD),
(AB+CD),
∴x+m=4,
∴m=4﹣x,
∴DFCF=((4﹣x)(2x﹣4)=﹣2x2+12x﹣16=﹣2(x﹣3)2+2,
∵﹣2<0,
∴x=3时,DFCF的值最大,最大值为2.


科目:初中数学 来源: 题型:
【题目】已知线段![]() ,点M是线段
,点M是线段![]() 上一动点,以
上一动点,以![]() 为直径作
为直径作![]() ,点C是圆周上一点且
,点C是圆周上一点且![]() ,连接
,连接![]() ,过点A做直线
,过点A做直线![]() 的垂线,交
的垂线,交![]() 于点N,连接
于点N,连接![]() ,设线段
,设线段![]() 的长为
的长为![]() ,线段
,线段![]() 的长为
的长为![]() ,线段
,线段![]() 的长为
的长为![]() .
.

小华同学根据学习函数的经验,分别对函数![]() ,随自变量x的变化而变化的规律进行了探究.
,随自变量x的变化而变化的规律进行了探究.
下面是该同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了![]() 与x的几组对应值:
与x的几组对应值:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 4.47 | 5.24 | 5.86 | 5.96 | 4.72 | 4.00 | |
| 6.00 | 5.86 | 5.23 | 3.98 | 2.46 | 1.06 | 0 |
请你补全表格的相关数值,保留两位小数.
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,
,![]() ,并画出函数
,并画出函数![]() 的图象(函数
的图象(函数![]() 的图象如图,请你画出
的图象如图,请你画出![]() 的图象)
的图象)
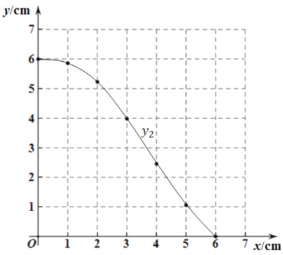
(3)结合画出的函数图象,解决问题:当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长度约为______
的长度约为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 动点
动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒
秒![]() ,连接
,连接![]() .若以
.若以![]() 为直径的
为直径的![]() 与
与![]() 的边相切,则
的边相切,则![]() 的值为_______.
的值为_______.
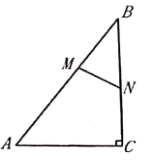
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,六边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
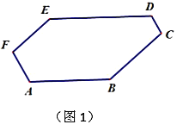
(1)找出这个六边形中所有相等的内角_______.证明其中的一个结论.
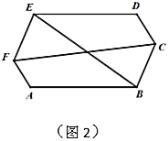
(2)如果![]() ,证明对角线
,证明对角线![]() ,
,![]() 互相平分;
互相平分;
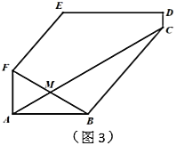
(3)如图,如果![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分对角线
平分对角线![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一黄金周,小张一家自驾去某景点旅行.已知汽车油箱的容积为50L,小张爸爸把油箱加满油后到了离加油站200km的某景点,第二天沿原路返回.
(1)油箱加满油后,求汽车行驶的总路程s(单位:km)与平均耗油量b(单位L/km)的函数关系式;
(2)小张爸爸以平均每千米耗油0.1L的速度驾驶到达目的地,返程时由于下雨,降低了车速,此时平均每千米的耗油量增加了一倍.如果小张爸爸始终以此速度行驶,不需要加油能否返回原加油站?如果不能,至少还需加多少油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在疫情防控期间,某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液.如果购买100瓶免洗手消毒液和150瓶84消毒液,共需花费1500元;如果购买120瓶免洗手消毒液和160瓶84消毒液,共需花费1720元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)某药店出售免洗手消毒液,满150瓶免费赠送10瓶84消毒液.若学校从该药店购进免洗手消毒液和84消毒液共230瓶,恰好用去1700元,则学校购买免洗手消毒液多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

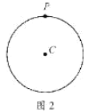
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
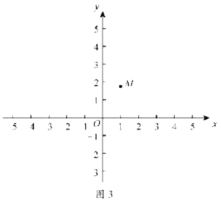
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com