
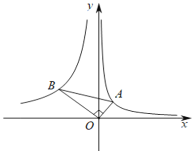
【题目】如图,Rt△AOB中,∠AOB=90°,![]() ,顶点A在反比例函数
,顶点A在反比例函数![]() 则点B所在的反比例函数解析式为_________.
则点B所在的反比例函数解析式为_________.
【答案】![]()
【解析】
分别过点A、B作x轴的垂线,根据∠AOB=90°,容易证得△BOD∽△OAC,设点A的坐标,由![]() 可得相似比为
可得相似比为![]() ,求得点B的坐标即可求出反比例函数的解析式.
,求得点B的坐标即可求出反比例函数的解析式.
过点A作AC⊥x轴,过点B作BD⊥x轴,分别交x轴于点C、点D,如图,
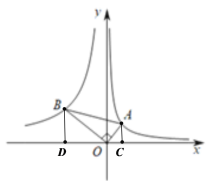
设A点坐标为![]() ,
,
则OC=a,AC=![]() ,
,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∵AC⊥OC,BD⊥OD,
∴∠BDO=∠ACO=90°,
∴∠AOC+∠OAC=90°,
∴∠BOD=∠OAC
∴△BOD∽△OAC,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴点B的坐标为![]() ,
,
设过点B的反比例函数的解析式为![]() ,代入点B的坐标可得,
,代入点B的坐标可得,
![]() ,
,
∴点B所在的反比例函数解析式为![]() ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】过直线外一点且与这条直线相切的圆称为这个点和这条直线的点线圆.特别地,半径最小的点线圆称为这个点和这条直线的最小点线圆.
在平面直角坐标系![]() 中,点
中,点![]() .
.
(1)已知点![]() ,
,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 为圆心,1为半径作
为圆心,1为半径作![]() ,
,![]() ,以
,以![]() 为圆心,2为半径作
为圆心,2为半径作![]() ,其中是点
,其中是点![]() 和
和![]() 轴的点线圆的是________;
轴的点线圆的是________;
(2)记点![]() 和
和![]() 轴的点线圆为
轴的点线圆为![]() ,如果
,如果![]() 与直线
与直线![]() 没有公共点,求
没有公共点,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)直接写岀点![]() 和直线
和直线![]() 的最小点线圆的圆心的横坐标
的最小点线圆的圆心的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小菲根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小菲的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是___________________.
的取值范围是___________________.
(2)下表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | … |
| … |
|
|
|
|
|
|
| 2 |
|
| … |
表中![]() 的值为____________________________.
的值为____________________________.
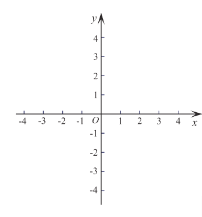
(3)如下图,在平面直角坐标系![]() 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
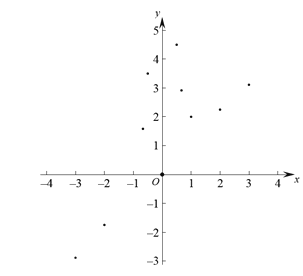
(4)根据画出的函数图象,写出:
①![]() 时,对应的函数值
时,对应的函数值![]() 约为__________________(结果保留一位小数);
约为__________________(结果保留一位小数);
②该函数的一条性质:________________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
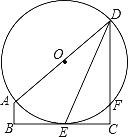
【题目】如图,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD为直径的⊙O与BC相切于点E,交CD于点F,连接DE.
(1)证明:DE平分∠ADC;
(2)已知AD=4,设CD的长为x(2<x<4).
①当x=2.5时,求弦DE的长度;
②当x为何值时,DFFC的值最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=ax2﹣4ax+a+1(a>0)
(1)若二次函数的图象与x轴有交点,求a的取值范围;
(2)若P(m,n)和Q(5,b)是抛物线上两点,且n>b,求实数m的取值范围;
(3)当m≤x≤m+2时,求y的最小值(用含a、m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2010河南20题)为鼓励学生参与体育锻炼,学校计划拿出不超过1600元的资金再购买一批篮球和排球.已知篮球和排球的单价比为![]() ,单价和为80元.
,单价和为80元.
(1)篮球和排球的单价分别是多少元?
(2)若要求购买的篮球和排球的总数量是36个,且购买的篮球的数量多于25个,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
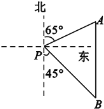
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,则这时海轮所在的B处距离灯塔P的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,对于给定的![]() ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为![]() 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为![]() 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
的完美内切弧.(注:弧的半径指该弧所在圆的半径)
在平面直角坐标系![]() 中,
中,![]() .
.
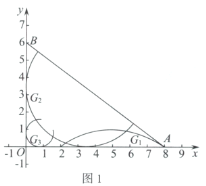
(1)如图1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的内切弧的是____________;
的内切弧的是____________;
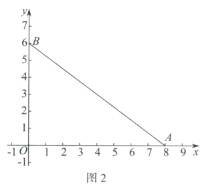
(2)如图2,若弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,求弧G的半径的最大值;
相切,求弧G的半径的最大值;
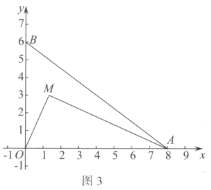
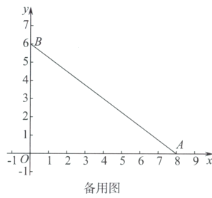
(3)如图3,动点![]() ,连接
,连接![]() .
.
①直接写出![]() 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T.点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线![]() 于点D,E,点F为线段
于点D,E,点F为线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com