
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

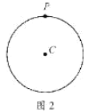
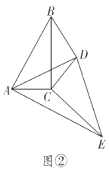
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
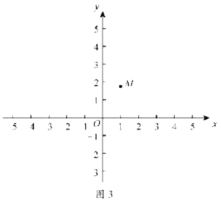
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
【答案】(1)详见解析;(2)①![]() 或
或![]() ;②
;②![]()
【解析】
(1)由题意当点P在在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,则圆心角∠ACB=120°,由此作图即可;
的关联点”时,则圆心角∠ACB=120°,由此作图即可;
(2)①设点P(0,y),连接MP,NP,MN交y轴于点Q,由题意及对称性可得△PMN为等边三角形,然后根据锐角三角函数值求PQ的长,从而确定点P的坐标;
②考虑临界情况,即恰好M、N点为⊙D的关联时,确定点D的坐标,从而求其取值范围.
解:(1)补全图形
由题意可知,∠APB=60°,点P在圆上
∴∠ACB=120°

(2)①设点P(0,y),连接MP,NP,MN交y轴于点Q
由题意可知,∠MPN=60°
又∵点M关于y轴的对称点为点N
∴△PMN为等边三角形
∴在Rt△MPQ中,![]()
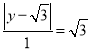 ,解得:
,解得:![]() 或0
或0
∴![]() 或
或![]()
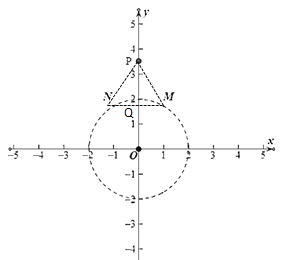
②当点D位于M点右侧且点M在圆上时,此时m有最大值,
由题意可知,此时∠OMD=60°,∴m=2
当点D位于N点左侧且点N在圆上时,此时m有最小值,
由题意可知,此时∠OMD=60°,∴m=-2
∴![]()



 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
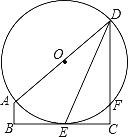
【题目】如图,在直角梯形ABCD中,AB∥CD,∠C=90°,以AD为直径的⊙O与BC相切于点E,交CD于点F,连接DE.
(1)证明:DE平分∠ADC;
(2)已知AD=4,设CD的长为x(2<x<4).
①当x=2.5时,求弦DE的长度;
②当x为何值时,DFFC的值最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,则这时海轮所在的B处距离灯塔P的距离是( )
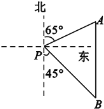
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC的顶点O是直角坐标系的原点,点A、C分别在x轴、y轴上,点B的坐标为(8,4),将矩形OABC绕点A顺时针旋转得到矩形ADEF,D、E、F分别与B、C、O对应,EF的延长线恰好经过点C,AF与BC相交于点Q.
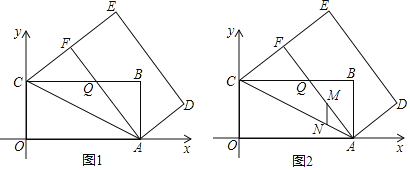
(1)证明:△ACQ是等腰三角形;
(2)求点D的坐标;
(3)如图2,动点M从点A出发在折线AFC上运动(不与A、C重合),经过的路程为x,过点M作AO的垂线交AC于点N,记线段MN在运动过程中扫过的面积为S;求S关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
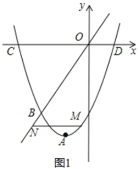
【题目】已知抛物线的顶点![]() ,经过点
,经过点![]() ,与
,与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
(2)如图1,点![]() 是抛物线上的一个动点,且在直线
是抛物线上的一个动点,且在直线![]() 的下方,过点
的下方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
(3)如图2,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时.
运动时.
①直接写出![]() 的值;
的值;
②直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,有五个点
中,有五个点![]() ,将二次函数
,将二次函数![]() 的图象记为W.下列的判断中
的图象记为W.下列的判断中
①点A一定不在W上;
②点B,C,D可以同时在W上;
③点C,E不可能同时在W上.
所有正确结论的序号是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,对于给定的![]() ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为![]() 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为![]() 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
的完美内切弧.(注:弧的半径指该弧所在圆的半径)
在平面直角坐标系![]() 中,
中,![]() .
.
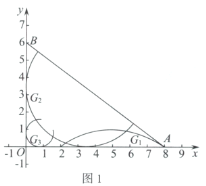
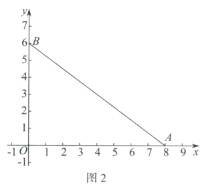
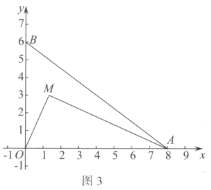
(1)如图1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的内切弧的是____________;
的内切弧的是____________;
(2)如图2,若弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,求弧G的半径的最大值;
相切,求弧G的半径的最大值;
(3)如图3,动点![]() ,连接
,连接![]() .
.
①直接写出![]() 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T.点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线![]() 于点D,E,点F为线段
于点D,E,点F为线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
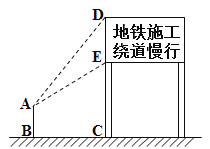
【题目】某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°.求路况指示牌DE的高度.(精确到0.01米,参考数据:![]() ≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,![]() 和
和![]() 是两个全等的直角三角形纸片,其中
是两个全等的直角三角形纸片,其中![]() ,
,![]() ,
,![]() .
.
解决问题
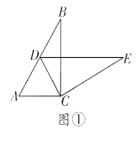
(1)如图①,智慧小组将![]() 绕点
绕点![]() 顺时针旋转,发现当点
顺时针旋转,发现当点![]() 恰好落在
恰好落在![]() 边上时,
边上时,![]() ,请你帮他们证明这个结论;
,请你帮他们证明这个结论;
(2)缜密小组在智慧小组的基础上继续探究,连接![]() ,当
,当![]() C绕点
C绕点![]() 继续旋转到如图②所示的位置时,他们提出
继续旋转到如图②所示的位置时,他们提出![]() ,请你帮他们验证这一结论是否正确,并说明理由;
,请你帮他们验证这一结论是否正确,并说明理由;
探索发现
(3)如图③,勤奋小组在前两个小组的启发下,继续旋转![]() ,当
,当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(4)在图①的基础上,写出一个边长比为![]() 的三角形(可添加字母).
的三角形(可添加字母).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com