
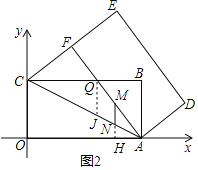
【题目】如图1,矩形OABC的顶点O是直角坐标系的原点,点A、C分别在x轴、y轴上,点B的坐标为(8,4),将矩形OABC绕点A顺时针旋转得到矩形ADEF,D、E、F分别与B、C、O对应,EF的延长线恰好经过点C,AF与BC相交于点Q.
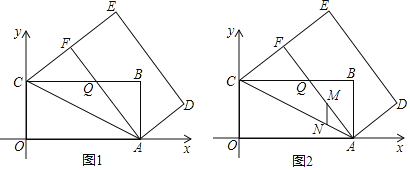
(1)证明:△ACQ是等腰三角形;
(2)求点D的坐标;
(3)如图2,动点M从点A出发在折线AFC上运动(不与A、C重合),经过的路程为x,过点M作AO的垂线交AC于点N,记线段MN在运动过程中扫过的面积为S;求S关于x的函数关系式.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)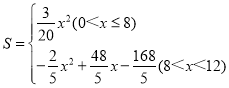
【解析】
(1)想办法证明∠QCA=∠QAC即可解决问题.
(2)设CQ=AQ=x,利用勾股定理求出x,如图1中,过点D作DH⊥x轴于H.利用相似三角形的性质求出AH,DH即可解决问题.
(3)分两种情形:①当0<x≤8时,如图2中,延长MN交AO于H,作QJ∥AB交AC于J.利用相似三角形的性质求出AH,MN即可解决问题.②当8<x<12时,如图3中,作QJ∥AB交AC于J,作EK∥AB交BC于T,设MN交BC于R.利用相似三角形的性质求出MN,AR即可解决问题.
(1)证明:∵四边形OABC,四边形FADE都是矩形,
∴∠AOC=90°,∠AFE=∠AFC=90°,BC∥OA,
∵∠CFA=∠AOC=90°,AC=AC,AO=AF,
∴Rt△ACO≌Rt△ACF(HL),
∴∠CAO=∠CAF,
∵BC∥OA,
∴∠BCA=∠CAO,
∴∠BCA=∠ACF,
∴QC=QA,
∴△ACQ是等腰三角形.
(2)解:设CQ=AQ=x,
∵B(8,4),
∴BC=8,AB=4,
在Rt△AQB中,∵AQ2=BQ2+AB2,
∴x2=(8﹣x)2+42,
∴x=5,
∴BQ=3,
如图1中,过点D作DH⊥x轴于H.
∵∠QAD=∠BAH=90°,
∴∠QAB=∠DAH,
∵∠B=∠AHD=90°,
∴△ABQ∽△AHD,
∴![]() ,
,
∴![]() ,
,
∴AH=![]() ,DH=
,DH=![]() ,
,
∴OH=OA+AH=8+![]() =
=![]() ,
,
∴D(![]() ).
).
(3)①当0<x≤8时,如图2中,延长MN交AO于H,作QJ∥AB交AC于J.
∵QJ∥AB,
∴![]() ,
,
∴![]() ,
,
∴QJ=![]() ,
,
∵MN∥QJ,
∴△AMN∽△AQJ,
∴![]() ,
,
∴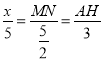
∴MN=![]() ,AH=
,AH=![]() ,
,
∴S=![]() MNAH=
MNAH=![]() ·
·![]() x·
x·![]() =
=![]() x2.
x2.
②当8<x<12时,如图3中,作QJ∥AB交AC于J,作EK∥AB交BC于T,设MN交BC于R.
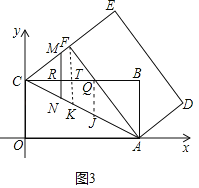
∵FK∥AB,JQ∥AB,
∴FK∥JQ,
∴△AQJ∽△AFK,
∴![]() ,
,
∴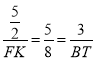 ,
,
∴FK=4,BT=![]() ,
,
∴CT=BC﹣BT=8﹣![]() =
=![]() ,
,
∵MN∥FK,
∴△CMN∽△CFK,
∴![]() ,
,
∴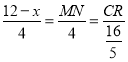 ,
,
∴MN=12﹣x,CR=![]() (12﹣x),
(12﹣x),
∴S=S△ACF﹣S△AFK=![]() ×4×12﹣
×4×12﹣![]() ×(12﹣x)×
×(12﹣x)×![]() (12﹣x)=
(12﹣x)=![]() .
.
综上所述,S=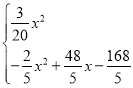
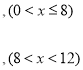 .
.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在疫情防控期间,某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液.如果购买100瓶免洗手消毒液和150瓶84消毒液,共需花费1500元;如果购买120瓶免洗手消毒液和160瓶84消毒液,共需花费1720元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)某药店出售免洗手消毒液,满150瓶免费赠送10瓶84消毒液.若学校从该药店购进免洗手消毒液和84消毒液共230瓶,恰好用去1700元,则学校购买免洗手消毒液多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
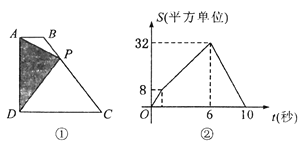
【题目】如图①,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 从
从![]() 点出发,以每秒2个单位长度的速度,按
点出发,以每秒2个单位长度的速度,按![]() 的顺序在边上匀速运动,设
的顺序在边上匀速运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,
,![]() 关于
关于![]() 的函数图像如图②所示,当
的函数图像如图②所示,当![]() 运动到
运动到![]() 中点时,
中点时,![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
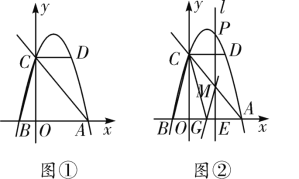
【题目】如图①,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)经过点D(2,4),与x轴交于A,B两点,与y轴交于点C(0,4),连接AC,CD,BC, 其且AC=5.
(1)求抛物线的解析式;
(2)如图②,点P是抛物线上的一个动点,过点P作x轴的垂线l,l分别交x轴于点E,交直线AC于点M.设点P的横坐标为m.当0<m≤2时,过点M作MG∥BC,MG交x轴于点G,连接GC,则m为何值时,△GMC的面积取得最大值,并求出这个最大值;
(3)当-1<m≤2时,是否存在实数m,使得以P,C,M为顶点的三角形和△AEM相似?若存在,求出相应m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

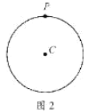
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
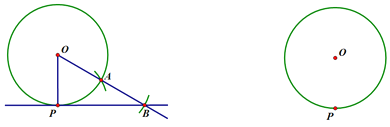
【题目】已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)请证明小明作法的正确性;
(2)请你自己再设计一种尺规作图方法(保留痕迹,不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍,在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示:

(1)求y与x之间的函数表达式,并写出自变量x的取值范围;
(2)该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式;并求出这种商品销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com