
【题目】已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
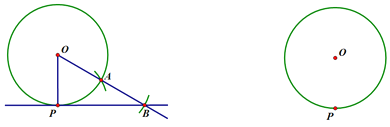
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)请证明小明作法的正确性;
(2)请你自己再设计一种尺规作图方法(保留痕迹,不要证明).
【答案】(1)见解析;(2)见解析;
【解析】
(1)连接![]() ,证出
,证出![]() 即可;
即可;
(2)先作一条射线OP,然后在OP外取一点A, 再以点A为圆心,AP为半径作圆,与射线OP交于另一点B,连接并延长BA与⊙A交于点C,连接PC即可.
证明:(1)连接![]() ,由题意可知:
,由题意可知:![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]()
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
即:![]() 为⊙O的切线;
为⊙O的切线;
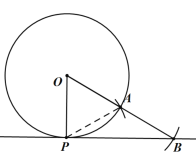
(2)解:作法:
①作射线OP;
②在射线OP外任取一点A, 以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.如下图所示:
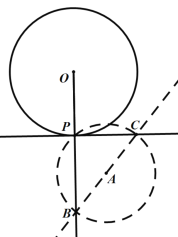
证明:∵BC是⊙A的直径,
∴∠BPC=90° (圆周角定理 ) ,
即OP⊥PC,
又∵OP是⊙O的半径,
∴PC是⊙O的切线(切线的判定) .


科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC的顶点O是直角坐标系的原点,点A、C分别在x轴、y轴上,点B的坐标为(8,4),将矩形OABC绕点A顺时针旋转得到矩形ADEF,D、E、F分别与B、C、O对应,EF的延长线恰好经过点C,AF与BC相交于点Q.
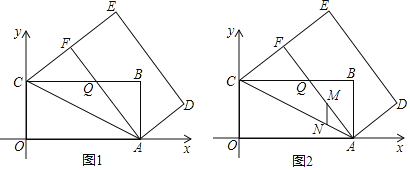
(1)证明:△ACQ是等腰三角形;
(2)求点D的坐标;
(3)如图2,动点M从点A出发在折线AFC上运动(不与A、C重合),经过的路程为x,过点M作AO的垂线交AC于点N,记线段MN在运动过程中扫过的面积为S;求S关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
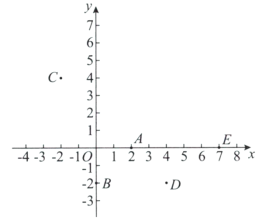
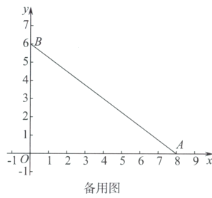
【题目】如图,在平面直角坐标系![]() 中,有五个点
中,有五个点![]() ,将二次函数
,将二次函数![]() 的图象记为W.下列的判断中
的图象记为W.下列的判断中
①点A一定不在W上;
②点B,C,D可以同时在W上;
③点C,E不可能同时在W上.
所有正确结论的序号是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,对于给定的![]() ,如果存在一个半圆或优弧与
,如果存在一个半圆或优弧与![]() 的两边相切,且该弧上的所有点都在
的两边相切,且该弧上的所有点都在![]() 的内部或边上,则称这样的弧为
的内部或边上,则称这样的弧为![]() 的内切弧.当内切弧的半径最大时,称该内切弧为
的内切弧.当内切弧的半径最大时,称该内切弧为![]() 的完美内切弧.(注:弧的半径指该弧所在圆的半径)
的完美内切弧.(注:弧的半径指该弧所在圆的半径)
在平面直角坐标系![]() 中,
中,![]() .
.
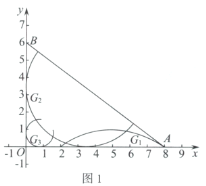
(1)如图1,在弧![]() ,弧
,弧![]() ,弧
,弧![]() 中,是
中,是![]() 的内切弧的是____________;
的内切弧的是____________;
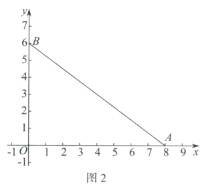
(2)如图2,若弧G为![]() 的内切弧,且弧G与边
的内切弧,且弧G与边![]() 相切,求弧G的半径的最大值;
相切,求弧G的半径的最大值;
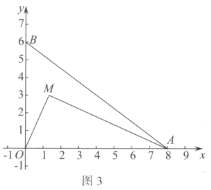
(3)如图3,动点![]() ,连接
,连接![]() .
.
①直接写出![]() 的完美内切弧的半径的最大值;
的完美内切弧的半径的最大值;
②记①中得到的半径最大时的完美内切弧为弧T.点P为弧T上的一个动点,过点P作x轴的垂线,分别交x轴和直线![]() 于点D,E,点F为线段
于点D,E,点F为线段![]() 的中点,直接写出线段
的中点,直接写出线段![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
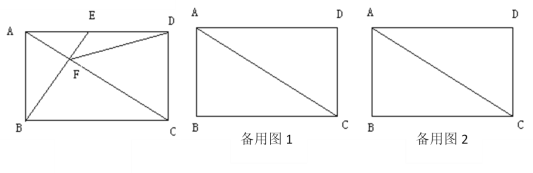
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E在AD上,BE与AC交于点F.
(1)若AC⊥BE,求AE的长 ;
(2)设△DEF和△DCF的面积分别为S1和S2,当AE=m时,求S1:S2;
(3)当AE的长是多少时,△DCF是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
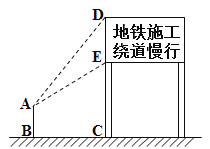
【题目】某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°.求路况指示牌DE的高度.(精确到0.01米,参考数据:![]() ≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
查看答案和解析>>
科目:初中数学 来源: 题型:
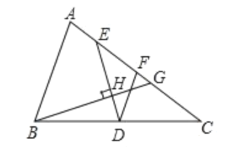
【题目】如图,在![]() 中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且
中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且![]() 与四边形ABDE的周长相等,设AC=b,AB=c.
与四边形ABDE的周长相等,设AC=b,AB=c.
(1)求线段CE的长度;
(2)求证:DF=EF;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖“综合与实践”小组学习了三角函数后,开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,如表是不完整测量数据.
课题 | 测量旗杆的高度 | |||
成员 | 组长:小颖,组员:小明,小刚,小英 | |||
测量工具 | 测量角度的仪器,皮尺等 | |||
测量示意图 |
| 说明: 线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.62m,测点A,B与H在同一水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
∠GCE的度数 | 30.6° | 31.4° | 31° | |
∠GDE的度数 | 36.8° | 37.2° | 37° | |
A,B之间的距离 | 10.1m | 10.5m | m | |
… | … | |||
(1)任务一:完成表格中两次测点A,B之间的距离的平均值.
(2)任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(精确到0.1m)(参考数据:sin31°≈0.51,cos31°≈0.86,tan31°≈0.60,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com