
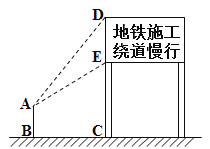
【题目】某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°.求路况指示牌DE的高度.(精确到0.01米,参考数据:![]() ≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
科目:初中数学 来源: 题型:
【题目】在疫情防控期间,某中学为保障广大师生生命健康安全购进一批免洗手消毒液和84消毒液.如果购买100瓶免洗手消毒液和150瓶84消毒液,共需花费1500元;如果购买120瓶免洗手消毒液和160瓶84消毒液,共需花费1720元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)某药店出售免洗手消毒液,满150瓶免费赠送10瓶84消毒液.若学校从该药店购进免洗手消毒液和84消毒液共230瓶,恰好用去1700元,则学校购买免洗手消毒液多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P是平面内任意一点,点A,B是![]() 上不重合的两个点,连结
上不重合的两个点,连结![]() .当
.当![]() 时,我们称点P为
时,我们称点P为![]() 的“关于
的“关于![]() 的关联点”.
的关联点”.

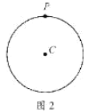
(1)如图2,当点P在![]() 上时,点P是
上时,点P是![]() 的“关于
的“关于![]() 的关联点”时,画出一个满足条件的
的关联点”时,画出一个满足条件的![]() ,并直接写出
,并直接写出![]() 的度数;
的度数;
(2)在平面直角坐标系中有点![]() ,点M关于y轴的对称点为点N.
,点M关于y轴的对称点为点N.
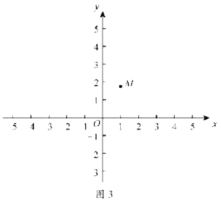
①以点O为圆心,![]() 为半径画
为半径画![]() ,在y轴上存在一点P,使点P为
,在y轴上存在一点P,使点P为![]() “关于
“关于![]() 的关联点”,直接写出点P的坐标;
的关联点”,直接写出点P的坐标;
②点![]() 是x轴上一动点,当
是x轴上一动点,当![]() 的半径为1时,线段
的半径为1时,线段![]() 上至少存在一点是
上至少存在一点是![]() 的“关于某两个点的关联点”,求m的取值范围.
的“关于某两个点的关联点”,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
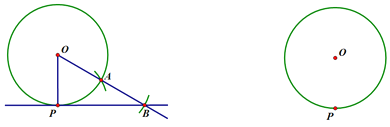
【题目】已知⊙O及⊙O上一点P,过点P作⊙O的切线.
小明设计了如下尺规作法:
①连接OP,以点P为圆心,OP长为半径画弧交⊙O于点A;
②连接OA,延长OA到B,使AB=OA,作直线PB.则直线即为所求作.
(1)请证明小明作法的正确性;
(2)请你自己再设计一种尺规作图方法(保留痕迹,不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在趣味运动会“定点投篮”项目中,我校七年级八个班的投篮成绩![]() 单位:个
单位:个![]() 分别为:24,20,19,20,22,23,20,
分别为:24,20,19,20,22,23,20,![]() 则这组数据中的众数和中位数分别是
则这组数据中的众数和中位数分别是![]()
![]()
A. 22个、20个 B. 22个、21个 C. 20个、21个 D. 20个、22个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在![]() 中,
中,![]() 把
把![]() 沿对角线
沿对角线![]() 所在的直线折叠,使点
所在的直线折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.
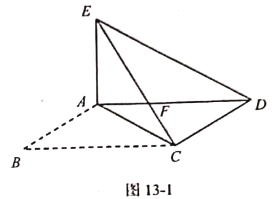
(1)求证:![]() ;
;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
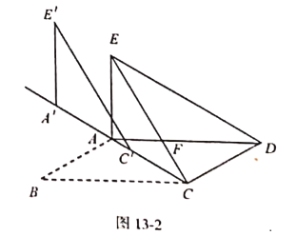
(3)将图1中![]() 的沿射线
的沿射线![]() 方向平移得到
方向平移得到![]() (如图2所示) .若在
(如图2所示) .若在![]() 中,
中,![]() . 当
. 当![]() 时,直接写出
时,直接写出![]() 平移的距离.
平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD内部有若干个点,则用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
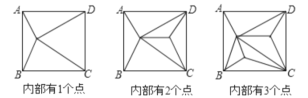
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | ... | n |
分割成三角形的个数 | 4 | 6 | _____ | _____ | ... | _____ |
(2)原正方形能否被分割成2021个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍,在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示:

(1)求y与x之间的函数表达式,并写出自变量x的取值范围;
(2)该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式;并求出这种商品销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
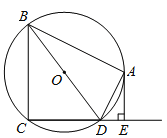
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com