【题目】如图①，四边形
中，
，
，
从
点出发，以每秒2个单位长度的速度，按
的顺序在边上匀速运动，设点的运动时间为
秒，
的面积为
，关于的函数图像如图②所示，当运动到
中点时，的面积为__________．
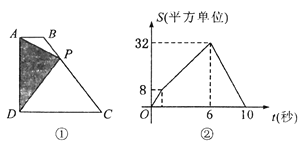
【答案】20
【解析】
由函数图象上的点（6，32）、（10，0）的实际意义可知AB+BC、AB+BC+CD的长及△PAD的最大面积，从而求得AD、CD的长，再根据点P运动到点B时得
，从而求得AB的长，最后根据梯形的中位线定理可求得当P运动到BC中点时，△PAD的面积．
解：由图象可知，AB+BC=12，AB+BC+CD=20，
∴CD=8，
根据题意可知，当P点运动到C点时，△PAD的面积最大，
， ∴AD=8，
又∵
，
∴AB=2，
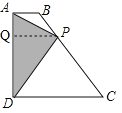
当P点运动到BC中点时，BP=PC，
如图，作PQ⊥AD于点Q，
∴AB∥PQ∥CD，
∴PQ为梯形ABCD的中位线，
则PQ= 
，
∴△PAD的面积=
故答案为：20．
走进文言文系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点
，在
轴上任取一点
，连接
，作的垂直平分线
，过点作轴的垂线
，与交于点
．设点的坐标为
．
（Ⅰ）当的坐标取
时，点的坐标为________；
（Ⅱ）求，
满足的关系式；
（Ⅲ）是否存在点，使得
恰为等边三角形？若存在，求点的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，分别以顶点A、B为圆心，大于
AB为半径作弧，两弧在直线AB两侧分别交于M、N两点，过M、N作直线MN，与AB交于点O，以O为圆心，OA为半径作圆，⊙O恰好经过点C．下列结论中，错误的是（ ）
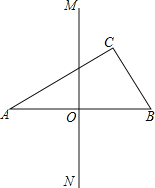
A.AB是⊙O的直径B.∠ACB＝90°
C.△ABC是⊙O内接三角形D.O是△ABC的内心
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司经过市场调查，发现某种运动服的销量与售价是一次函数关系，具体信息如下表：
售价（元/件） | 200 | 210 | 220 | 230 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元．
（1）售价为
元，月销量为
件；
①求关于的函数关系式；
②若销售该运动服的月利润为
元，求关于的函数关系式，并求月利润最大时的售价；
（2）由于运动服进价降低了
元，商家决定回馈顾客，打折销售，这时月销量与调整后的售价仍满足（1）中函数关系式．结果发现，此时月利润最大时的售价比调整前月利润最大时的售价低15元，则的值是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
内接于⊙
，直径
交
于点
，连接
，过点
作
，垂足为
．过点
作⊙的切线，交
的延长线于点
．
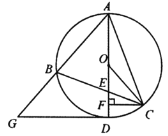
(1)若
，求
的度数；
(2)若
，求证：
；
(3)在(2)的条件下，连接
，设
的面积为
，
的面积为
，若
，求
的值
查看答案和解析>>
科目：初中数学 来源： 题型：
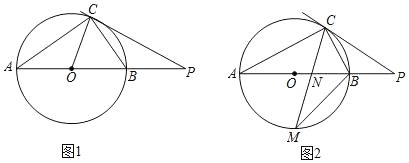
【题目】已知，AB是⊙O的直径，点C在⊙O上，点P是AB延长线上一点，连接CP．
(1)如图1，若∠PCB＝∠A．
①求证：直线PC是⊙O的切线；
②若CP＝CA，OA＝2，求CP的长；
(2)如图2，若点M是弧AB的中点，CM交AB于点N，MNMC＝9，求BM的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
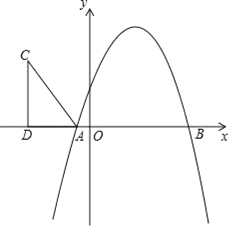
【题目】如图，抛物线y＝－x2＋bx＋c与x轴相交于A（－1，0），B（5，0）两点．
（1）求抛物线的解析式；
（2）在第二象限内取一点C，作CD垂直x轴于点D，链接AC，且AD＝5，CD＝8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；
（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
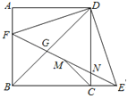
【题目】如图，正方形ABCD中，F为AB上一点，E是BC延长线上一点，且AF＝EC，连结EF，DE，DF，M是FE中点，连结MC，设FE与DC相交于点N．则4个结论：①DE＝DF；②∠CME=∠CDE；③DG2=GN GE；④若BF＝2，
则正确的结论有（ ）个．
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
