
【题目】在平面直角坐标系中,点![]() ,在
,在![]() 轴上任取一点
轴上任取一点![]() ,连接
,连接![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,
,![]() 与
与![]() 交于点
交于点![]() .设
.设![]() 点的坐标为
点的坐标为![]() .
.
(Ⅰ)当![]() 的坐标取
的坐标取![]() 时,点
时,点![]() 的坐标为________;
的坐标为________;
(Ⅱ)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(Ⅲ)是否存在点![]() ,使得
,使得![]() 恰为等边三角形?若存在,求点
恰为等边三角形?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)存在,
;(Ⅲ)存在,![]() ,
, ![]() .
.
【解析】
(Ⅰ)作AN⊥PM于N,根据线段垂直平分线的性质得到PA=PM,根据勾股定理计算;
(Ⅱ)分点M在x轴的正半轴上、点M在x轴的负半轴上两种情况,根据勾股定理列式计算;
(Ⅲ)根据勾股定理求出MA,根据(Ⅱ)中结论列出方程,解方程即可.
(Ⅰ)作AN⊥PM于N,
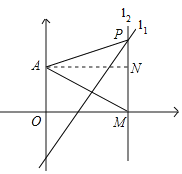
则四边形AOMN是矩形,
∴AN=OM=3,MN=OA=2,
∵l1是AM的垂直平分线,
∴PA=PM,
在Rt△APN中,AN2+PN2=AP2,即32+(y-2)2=y2,
解得,y=![]() ,
,
∴点P的坐标为(3,![]() ),
),
故答案为:(3,![]() );
);
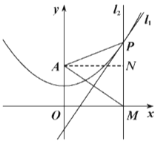
(Ⅱ)如图,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
可得![]() 为矩形,可得
为矩形,可得![]() ,
,
∵![]() 轴,
轴,![]() 点的坐标为
点的坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 在
在![]() 的垂直平分线
的垂直平分线![]() 上,
上,
∴![]() ,
,
在![]() 中,
中,![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() .
.
(Ⅲ)由(Ⅱ)知,![]() ,要使△MPA为等边三角形,只需MA=MP即可,
,要使△MPA为等边三角形,只需MA=MP即可,
∵点A的坐标为(0,2),点M的坐标为(0,x),
∴AM=![]() ,
,
则![]() ,
,
解得,x=±2![]() ,
,
∴![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
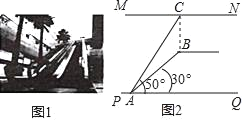
【题目】如图1是某商场从一楼到二楼的自动扶梯,图2是侧面示意图,MN是二楼楼顶,MN∥PQ,点C在MN上,且位于自动扶梯顶端B点的正上方,BC⊥MN.测得AB=10米,在自动扶梯底端A处测得点C的仰角为50°,点B的仰角为30°,求二楼的层高BC(结果保留根号)
(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
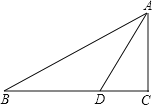
(1)用直尺和圆规在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;(友情提醒:必须作在答题卷上哦!)
(2)若AC=3,BC=4,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
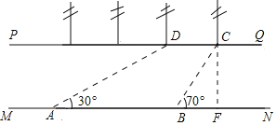
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来.
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
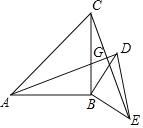
【题目】如图,△ABC和△BED都是等腰直角三角形,∠ABC=∠DBE=90°,AD,CE相交于点G
(1)求证:△ABD≌△CBE;
(2)求证:AD⊥CE;
(3)连接AE,CD,若AE=![]() CD=5,求△ABC和△BED的面积之和.
CD=5,求△ABC和△BED的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
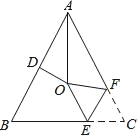
A. 106°B. 108°C. 110°D. 112°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() ,
,![]() ,
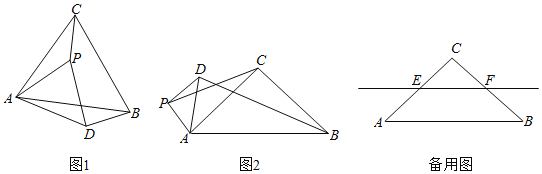
,![]() .点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.
(1)观察猜想
如图1,当![]() 时,
时,![]() 的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当![]() 时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时
时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
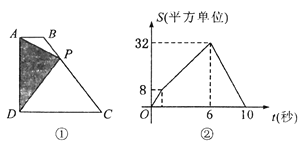
【题目】如图①,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 从
从![]() 点出发,以每秒2个单位长度的速度,按
点出发,以每秒2个单位长度的速度,按![]() 的顺序在边上匀速运动,设
的顺序在边上匀速运动,设![]() 点的运动时间为
点的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,
,![]() 关于
关于![]() 的函数图像如图②所示,当
的函数图像如图②所示,当![]() 运动到
运动到![]() 中点时,
中点时,![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com