
����Ŀ����1��СMyͬѧ������ֱ������ѧϰ�˹��ɶ������������һ֪ʶӦ���ڵȱ��������У��߳�Ϊa�ĵȱ�������������� �����ú�a�Ĵ���ʽ��ʾ����
��2��СMyͬѧ��һ��˼�����Ƿ���Խ������μ�ƴ��һ���ȱ������Σ����ص�����϶����
�������һ���߳�Ϊ2��������ֽƬ��ƴ�ȱ������Σ���ô�������α߳���ƽ������ ����
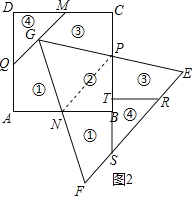
��СMyͬѧ����ͼ�и����������ABCD��ƴ��һ���ȱ�������EFG��M��N�ֱ�ΪAB��CD���ϵ��е㣬P��Q�DZ�BC��AD�����㣬GΪMQ��һ�㣬�ҡ�MGP����PGN����NGQ��60�㣮
�벹ȫͼ�Σ�����ƴ���������εĸ����ַָ��ߣ�����ţ�
��������ABCD�ı߳�Ϊ2����BP��x����x2���� ����

���𰸡���1��![]() a2����2����
a2����2����![]() ���������������
���������������![]() ��1��
��1��
��������
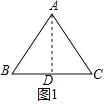
��1����ͼ1����A��AD��BC��D�����ݵȱ������ε����ʵõ�BD��CD��![]() BC��
BC��![]() a���ɹ��ɶ����õ�AD��
a���ɹ��ɶ����õ�AD��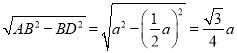 �����ǵõ�S��ABC��
�����ǵõ�S��ABC��![]() BCAD��
BCAD��![]() ��
��
��2�������������ε������ʽ���ɵõ����ۣ�
����ȫͼ����ͼ2��ʾ��
��������֪��PG��PE��GN��NF���Ƴ�PN�ǡ�GEF����λ�ߣ��õ�PN��![]() EF�����ݹ��ɶ������ɵõ����ۣ�
EF�����ݹ��ɶ������ɵõ����ۣ�
�⣺��1����ͼ����A��AD��BC��D��
�ߡ�ABC�ǵȱ������Σ�
��BD��CD��![]() BC��
BC��![]() a��
a��
��AD��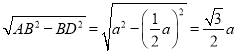 ��
��
��S��ABC��![]() BCAD��
BCAD��![]() a2��
a2��
��2�����߱߳�Ϊ2�������ε������4��
���ƴ�ɵĵȱ������ε������4��
��![]() a2��4��
a2��4��
��a2��![]() ��
��
���������α߳���ƽ����![]() ��
��
����ȫͼ����ͼ2��ʾ��
��������֪��PG��PE��GN��NF��
��PN�ǡ�GEF����λ�ߣ�
��PN��![]() EF��
EF��
��NΪAB���ϵ��е㣬
��BN��![]() AB��1��
AB��1��
�߱߳�Ϊ2�������ε������4��
���ƴ�ɵĵȱ������ε������4��
��![]() a2��4��
a2��4��
��a2��![]() ��
��
����GEF�߳���ƽ����![]() ��
��
��EF��![]() ��
��
��PN��![]() ��
��
��PN2��BN2+BP2��
��![]() ��1+x2��
��1+x2��
��x2��![]() ��1��
��1��
�ʴ�Ϊ����1��![]() ����2����
����2����![]() ����
����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�����㣬�ֱ���
�ϵ�һ�����㣬�ֱ���![]() ��
��![]() ����
Ϊ����![]() ��ͬ��������
��ͬ��������![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() ��һ��ֱ���ϣ�
��һ��ֱ���ϣ�![]() ��
��![]() ��
��![]() �ֱ��ǶԽ���
�ֱ��ǶԽ���![]() ��
��![]() ���е㣬����
���е㣬����![]() ���߶�
���߶�![]() ���ƶ�ʱ���߶�
���ƶ�ʱ���߶�![]() ����СֵΪ________��
����СֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�� ![]() �;���
�;���![]() ��ͼ�ٰڷţ���
��ͼ�ٰڷţ���![]() ���
���![]() �غϣ�����
�غϣ�����![]() ��
�� ![]() ��ͬһֱ���ϣ�
��ͬһֱ���ϣ� ![]() ��
�� ![]() ��
�� ![]() .��ͼ�ڣ�
.��ͼ�ڣ�![]() ��ͼ�ٵ�λ�ó�������
��ͼ�ٵ�λ�ó�������![]() ���������˶����ٶ�Ϊ1
���������˶����ٶ�Ϊ1 ![]() ��
�� ![]() ��
��![]() ���ڵ�
���ڵ�![]() ����BD���ڵ�K��ͬʱ����
����BD���ڵ�K��ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ1
���������˶����ٶ�Ϊ1 ![]() .����
.����![]() ��
��![]() ������Ϊ
������Ϊ![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ֹͣ�˶�ʱ��
ֹͣ�˶�ʱ�� ![]() Ҳֹͣ�˶�.���˶��¼�Ϊ
Ҳֹͣ�˶�.���˶��¼�Ϊ![]() .����������⣺
.����������⣺
��1����Ϊ��ֵʱ�� ![]() ��
��
��2�����˶������У��Ƿ����ijһʱ�̣�ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵��������
��ֵ���������ڣ���˵��������
��3�����˶������У�
�ٵ�tΪ ��ʱ����PQΪֱ����Բ��PE���У�
�ڵ�tΪ ��ʱ����PQ���е�ΪԲ�ģ��� cmΪ�뾶��Բ��BD��BCͬʱ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��
��![]() ֮���һ�㣬����
֮���һ�㣬����![]() ��
��![]() .
.
��1��̽�����룺
����![]() ����
����![]() .
.
����![]() ����
����![]() .
.
������ͼ1��![]() ��
��![]() ��
��![]() �Ĺ�ϵ����֤����Ľ���.
�Ĺ�ϵ����֤����Ľ���.
��2����չӦ�ã�
��ͼ2��![]() ���߶�
���߶�![]() ��
��![]() �����������ΪI��II�����֣������߽磩����
�����������ΪI��II�����֣������߽磩����![]() ��λ�������������ڵ�����һ�㣬��ֱ��д��
��λ�������������ڵ�����һ�㣬��ֱ��д��![]() ��
��![]() ��
��![]() �Ĺ�ϵ.
�Ĺ�ϵ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2+bx+c��y=x��ͼ����ͼ��ʾ�������½��ۣ�
��b2��4c��0����b+c=0����2b+c+3=0������1��x��3ʱ��x2+��b��1��x+c��0
������ȷ���У�����������

A. 4 B. 3 C. 2 D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼA�������϶�Ӧ����Ϊ-2.
(1)��B�ڵ�A�ұ߾���A��4����λ���ȣ����B����Ӧ������_____.
(2)��(1)�������£���A��ÿ��2����λ���������������˶�����B��ÿ��3����λ���������������˶�.������ͬʱ�˶�,����A�˶���-6�ĵ㴦ʱ����A��B�����ľ���.
(3)��(2)�������£���A�㾲ֹ������B����ԭ�������������˶��������ʱ��A��B�������4����λ����.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��CD��MN�ֱ�AB��CD�ڵ�E��F����BEF���DFE������ƽ�����ཻ�ڵ�P1����BEP1���DFP1������ƽ�����ཻ�ڵ�P2�����P2�Ķ���Ϊ_______��
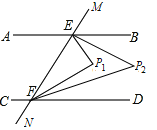
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ����С��������ɵļ����������ͼ����ͼ��

![]() �ü�����������Ҫ����С�����壿�������м���С�����壿
�ü�����������Ҫ����С�����壿�������м���С�����壿
![]() �뻭���ü���������п��ܵ�����ͼ��
�뻭���ü���������п��ܵ�����ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ΪԤ��������ijУ�Խ��ҽ�����ҩѬ����������֪ҩ��ȼ�սΣ�����ÿ���������еĺ�ҩ��![]() ��mg����ȼ��ʱ��
��mg����ȼ��ʱ��![]() �����ӣ�����������ȼ�պ�
�����ӣ�����������ȼ�պ� ![]() ��
��![]() �ɷ���������ͼ��ʾ�����ֲ��ҩ��10����ȼ�꣬��ʱ������ÿ����������ҩ��Ϊ8mg����������Ϣ����������⣺
�ɷ���������ͼ��ʾ�����ֲ��ҩ��10����ȼ�꣬��ʱ������ÿ����������ҩ��Ϊ8mg����������Ϣ����������⣺
��1����ҩ��ȼ��ʱ![]() ��
��![]() �ĺ�����ϵʽ����2����ҩ��ȼ�պ�
�ĺ�����ϵʽ����2����ҩ��ȼ�պ�![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����ÿ���������к�ҩ������1.6mgʱ�������巽���������ã���ô��������ʼ�����ʱ��ѧ���ſ��Իؽ��ң�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com