
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.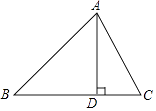
科目:初中数学 来源: 题型:
【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.有一组邻边相等的平行四边形是矩形
B.四条边相等的四边形是菱形
C.有一个角是直角的平行四边形是菱形
D.对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
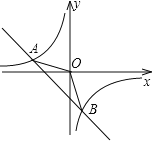
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣![]() <0的解集.
<0的解集.
(3)P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D′处,则重叠部分△AFC的面积是( ) 
A.8
B.10
C.20
D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以lcm/s的速度运动,同时点F从点B出发沿线射BC以2cm/s的速度运动,设运动时间为t(s). 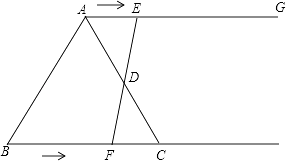
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)当t为多少时,四边形ACFE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com