练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小明想知道学校旗杆有多高，他发现旗杆上的绳子垂到地面还余1m，当他把绳子下端拉开5m后，发现下端刚好接触地面，则旗杆高度为_____米．

    【答案】12

    【解析】

    由题可知，旗杆，绳子与地面构成直角三角形，根据题中数据，用勾股定理即可解答．

    解：设旗杆高xm，则绳子长为（x+1）m，∵旗杆垂直于地面，

    ∴旗杆，绳子与地面构成直角三角形，由题意列式为x2+52=（x+1）2，解得x=12m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某班10名学生的校服尺寸与对应人数如表所示：

    尺寸（cm）

    160

    165

    170

    175

    180

    学生人数（人）

    1

    3

    2

    2

    2

    则这10名学生校服尺寸的众数和中位数分别为（ ）
    A.165cm，165cm
    B.165cm，170cm
    C.170cm，165cm
    D.170cm，170cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以下说法中正确的语句共有几个（　　） ①两点确定一条直线；
    ②延长直线AB到C；
    ③延长线段AB到C，使得AC=BC；
    ④反向延长线段BC到D，使BD=BC；
    ⑤线段AB与线段BA表示同一条线段；
    ⑥线段AB是直线AB的一部分．
    A.3
    B.4
    C.5
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：x2﹣x﹣20＝0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积． 某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．
    作AD⊥BC于D，设BD=x，用含x的代数式表示CD→根据勾股定理，利用AD作为“桥梁”，建立方程模型求出x→利用勾股定理求出AD的长，再计算三角形的面积．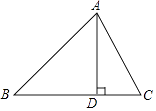

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点． 请解决下列问题：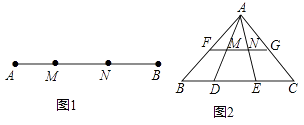

    （1）已知点M，N是线段AB的勾股分割点，且BN＞MN＞AM．若AM=2，MN=3，求BN的长；
    （2）如图2，若点F、M、N、G分别是AB、AD、AE、AC边上的中点，点D，E是线段BC的勾股分割点，且EC＞DE＞BD，求证：点M，N是线段FG的勾股分割点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：x2﹣9= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在儿时玩玩具手枪，在瞄准时总是半闭着眼，对着准星与目标，用数学知识解释为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

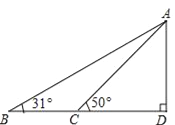
    【题目】据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪，如图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°.

    （1）求B，C的距离．

    （2）通过计算，判断此轿车是否超速．（tan31°≈0.6，tan50°≈1.2，结果精确到1m）

    查看答案和解析>>

    同步练习册答案