
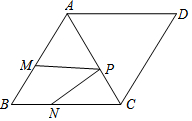
 已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$.
已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$. 分析 如图,作AH⊥BC于H.首先证明△ABC,△ADC的是等边三角形,作点M关于直线AC的对称点M′,因为PM+PN=PM′+PN,所以欲求PM+PN是最小值,只要求PM′+PN的最小值,所以根据垂线段最短,当M″、P、N′共线时,M″N′⊥BC时,PM″+PN′的值最小,易证四边形AHN′M″是矩形,所以N′M″=AH=AB•sin60°,由此即可解决问题.
解答 解:如图,作AH⊥BC于H.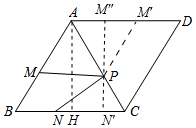
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=∠D=60°,
∴△ABC,△ADC的是等边三角形,
作点M关于直线AC的对称点M′,
∵PM+PN=PM′+PN,
∴欲求PM+PN是最小值,只要求PM′+PN的最小值,
∴根据垂线段最短,
当M″、P、N′共线时,M″N′⊥BC时,PM″+PN′的值最小,
易证四边形AHN′M″是矩形,
∴N′M″=AH=AB•sin60°=4$\sqrt{2}$•$\frac{\sqrt{3}}{2}$=2$\sqrt{6}$,
故答案为2$\sqrt{6}$.
点评 本题考查轴对称最短问题、菱形的性质、等边三角形的判定和性质、垂线段最短等知识,解题的关键是学会用转化的思想思考问题,把最短问题转化为垂线段最短,属于中考常考题型.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a5=a10 | B. | a2-2ab+b2=(a-b)2 | C. | -(a-b)=b-a | D. | 3a3b2÷a2b2=3a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 人员 | 经理 | 厨师 | 会计 | 保安 | 服务员 |
| 人数(人) | 1 | 2 | 1 | 1 | 5 |
| 工资(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
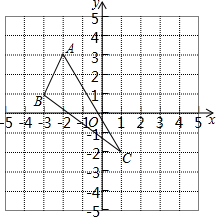 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{x-1}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{1}{16}}$ | D. | $\sqrt{9{a^2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
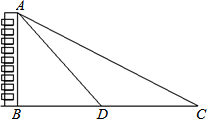 如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.
如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com