
【题目】先阅读,并探究相关的问题:
(阅读)
![]() 的几何意义是数轴上
的几何意义是数轴上![]() ,
,![]() 两数所对的点
两数所对的点![]() ,
,![]() 之间的距离,记作
之间的距离,记作![]() ,如
,如![]() 的几何意义:表示
的几何意义:表示![]() 与
与![]() 两数在数轴上所对应的两点之间的距离;
两数在数轴上所对应的两点之间的距离;![]() 可以看做
可以看做![]() ,几何意义可理解为
,几何意义可理解为![]() 与
与![]() 两数在数轴上对应的两点之间的距离.
两数在数轴上对应的两点之间的距离.
(1)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离可表示为____________;如果
之间的距离可表示为____________;如果![]() ,求出
,求出![]() 的值;
的值;
(2)探究:![]() 是否存在最小值,若存在,求出最小值;若不存在,请说明理由;
是否存在最小值,若存在,求出最小值;若不存在,请说明理由;
(3)求![]() 的最小值,并指出取最小值时
的最小值,并指出取最小值时![]() 的值.
的值.
![]()
【答案】(1)![]() ,x=3或7;
,x=3或7;
(2)最小值是5;
(3)当x=1010时,最小值为1019090.
【解析】
(1)根据两点间的距离公式直接计算即可;
(2)根据绝对值的几何意义求解即可;
(3)根据绝对值的几何意义,可得![]() 有最小值,当x=1010时,
有最小值,当x=1010时,![]() 的最小值为1019090.
的最小值为1019090.
(1)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离可表示为
之间的距离可表示为![]() ,
,
根据数轴上与表示2的点相距5个单位的点表示的数为3或7,可得若|x+2|=5,则x=3或7;
(2)若点P表示的数为x,当点P在数轴上-3≤x≤2位置时,|x+3|+|x2|有最小值,最小值是5;
(3)![]()
=![]()
要使|x1|+|x-2019|的值最小,x的值取1到2019之间(包括1、2019)的任意一个数,
要使|x2|+|x-2018|的值最小,x取2到2018之间(包括2、2018)的任意一个数,…
要使|x1009|+|x-1011|的值最小,x取1009到1011之间(包括1009、1011)的任意一个数,
要使|x1010|的值最小,x取1010,
把x=1010代入原式,
得![]()
=1009+1008+…+1+0+1+2+…+1008+1009=1019090,
即当x=1010时,最小值为1019090.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BE平分∠ABC,CD平分∠ACB,CD交BE 于点F,那么图中的等腰三角形共有( )个.
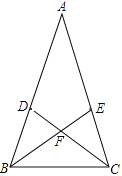
A. 6B. 7C. 8D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.
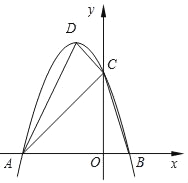
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列等式:①由a=b,得5﹣2a=5﹣2b;②由a=b,得ac=bc;③由a=b,得![]() ;④由
;④由![]() ,得3a=2b;
,得3a=2b;
⑤由a2=b2,得a=b.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线 y= -x+5交x轴于A,交y轴于B,直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)求四边形BODC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
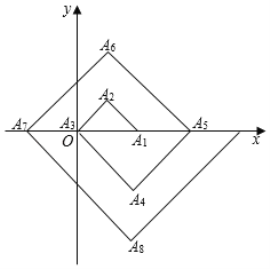
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
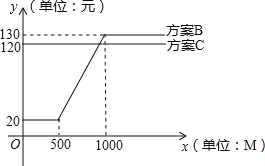
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com