
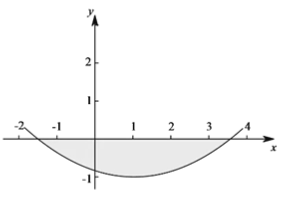
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.

【答案】(1)(1,-1);(2)①3;②![]() .
.
【解析】
试题分析:(1)将抛物线表达式变为顶点式,即可得到顶点坐标;
(2)①m=1时,抛物线表达式为![]() ,即可得到A、B的坐标,可得到线段AB上的整点个数;
,即可得到A、B的坐标,可得到线段AB上的整点个数;
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;令y=0,则![]() ,解方程可得到A、B两点坐标分别为(
,解方程可得到A、B两点坐标分别为(![]() ,0),(
,0),(![]() ,0),即5个整点是以(1,0)为中心向两侧分散,进而得到
,0),即5个整点是以(1,0)为中心向两侧分散,进而得到![]() ,即可得到结论.
,即可得到结论.
试题解析:(1)将抛物线表达式变为顶点式![]() ,则抛物线顶点坐标为(1,-1);
,则抛物线顶点坐标为(1,-1);
(2)①m=1时,抛物线表达式为![]() ,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;
,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;又有抛物线表达式,令y=0,则![]() ,得到A、B两点坐标分别为(
,得到A、B两点坐标分别为(![]() ,0),(
,0),(![]() ,0),即5个整点是以(1,0)为中心向两侧分散,进而得到
,0),即5个整点是以(1,0)为中心向两侧分散,进而得到![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABD和等边三角形CBD的边长均为a,现把它们拼合起来,E是AD上异于A、D两点的一动点,F是CD上一动点,满足AE+CF=a.则△BEF的形状如何?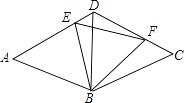
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数.求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( ) 
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校进行书法比赛,有39名同学参加预赛,只能有19名同学参加决赛,他们预赛的成绩各不相同,其中一名同学想知道自己能否进入决赛,不仅要了解自己的预赛成绩,还要了解这39名同学预赛成绩的( )
A.平均数
B.中位数
C.方差
D.众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
在计算器上输入一个正数,不断地按“![]() ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】
输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】
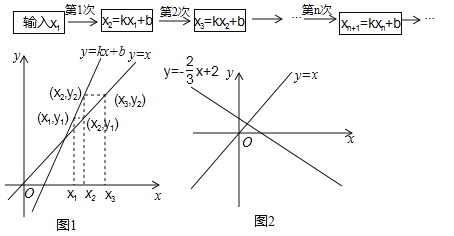
我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】
研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若![]() ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5,∴p=![]() =6,∴S=
=6,∴S=![]() =
=![]() =6.
=6.
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=x2+2x﹣3的开口方向、顶点坐标分别是( )
A.开口向上,顶点坐标为(﹣1,﹣4)
B.开口向下,顶点坐标为(1,4)
C.开口向上,顶点坐标为(1,4)
D.开口向下,顶点坐标为(﹣1,﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com