
【题目】如图![]() ,在平面直角坐标系中,抛物线
,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)过点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,若点
,若点![]() 是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点
是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,作
,作![]() 轴交对称轴于点
轴交对称轴于点![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,当矩形
,当矩形![]() 的周长最大时,在
的周长最大时,在![]() 轴上有一动点
轴上有一动点![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,一动点
,一动点![]() 从线段
从线段![]() 的中点
的中点![]() 出发以每秒
出发以每秒![]() 个单位的速度沿
个单位的速度沿![]() 的路径运动到点
的路径运动到点![]() ,再沿线段
,再沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 点处停止运动,求动点
点处停止运动,求动点![]() 运动时间的最小值:
运动时间的最小值:
(2)如图![]() , 将
, 将![]() 绕点
绕点![]() 顺时针旋转至
顺时针旋转至![]() 的位置, 点
的位置, 点![]() 的对应点分别为
的对应点分别为![]() ,且点
,且点![]() 恰好落在抛物线的对称轴上,连接
恰好落在抛物线的对称轴上,连接![]() .点
.点![]() 是
是![]() 轴上的一个动点,连接
轴上的一个动点,连接![]() , 将
, 将![]() 沿直线
沿直线![]() 翻折为
翻折为![]() , 是否存在点
, 是否存在点![]() , 使得
, 使得![]() 为等腰三角形?若存在,请求出点
为等腰三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
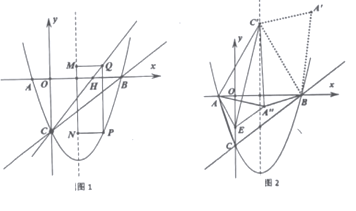
【答案】(1)![]() ;(2)(0,3-
;(2)(0,3-![]() )或(0,6)或(0,3+
)或(0,6)或(0,3+![]() )或(0,12).
)或(0,12).
【解析】
(1)根据题意设![]() ,
,![]() ,以及作
,以及作![]() 关于
关于![]() 轴对称
轴对称![]() ,并过
,并过![]() 点作直线
点作直线![]() 的垂线交于
的垂线交于![]() 点
点![]() 即为所求,从而进行分析求解即可;
即为所求,从而进行分析求解即可;
(2)根据题意分四种情形即①当AA'=A'B时;②当AA'=AB时;③当AA'=A'B时;④当A'B=AB时分别画出图形并进行分析求解.
解:(1)设![]() ,
,![]() ,
,
![]() ,
,
![]() ,开口向下,
,开口向下,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 最少时间
最少时间![]() ,
,
![]() ,作
,作![]() 关于
关于![]() 轴对称
轴对称![]() ,
,
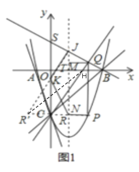
过![]() 点作直线
点作直线![]() 的垂线交于
的垂线交于![]() 点
点![]() 即为所求,
即为所求,
令y=0,解得![]()
![]() ,
,
![]() ,
,
![]() 过
过![]() 作
作![]() ,
,
![]() .
.
(2)①当AA'=A'B时,如图2中,
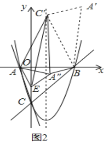
此时,A'在对称轴上
对称性可知∠AC′E=∠A'C′E
又∠HEC′=∠A'C′E
∴∠AC′E=∠HEC′
∴HE=HC'=5 ![]() 2
2 ![]() =3
=3 ![]() ,
,
∴OE=HE-HO=3 ![]() 3,
3,
∴E(0,33 ![]() ),
),
②当AA'=AB时,如图3中,设A″C′交y轴于J.
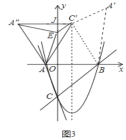
此时AA'=AB=BC'=A'C',
∴四边形A'ABC'为菱形,
由对称性可知,
∠AC'E=∠A'C'E=30°,
∴JE= ![]() JC′=
JC′=![]() ,
,
∴OE=OJ-JE=6
∴E(0,6)
③当AA'=A'B时,如图4中,设AC′交y轴于M.

此时,A'在对称轴上∠MC'E=75°
又∠AMO=∠EMC'=30°
∴∠MEC'=75°
∴ME=MC'
∴MC'=3 ![]() ,
,
∴OE=3+3 ![]() ,
,
∴E(0,3+![]() ).
).
④当A'B=AB时,如图5中,
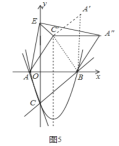
此时AC'=A'C'=A'B=AB
∴四边形AC'A'B为菱形
由对称性可知,C',E,B共线
由抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧)可知,
的左侧)可知,
令x=0,解得y=3 ![]() ;令x=0,解得:x1=
;令x=0,解得:x1= ![]() ,x2=4
,x2=4 ![]() ;
;
∴A(![]() ,0),B(4
,0),B(4![]() ,0),OB=4
,0),OB=4![]() ,
,
∴OE= ![]() OB=12,
OB=12,
∴E(0,12).
综上满足条件的点E坐标为(0,3-![]() )或(0,6)或(0,3+
)或(0,6)或(0,3+![]() )或(0,12).
)或(0,12).


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】(材料阅读)
我们曾解决过课本中的这样一道题目:
如图1,四边形ABCD是正方形,E为BC边上一点,延长BA至F,使AF=CE,连接DE,DF.……
提炼1:△ECD绕点D顺时针旋转90°得到△FAD;
提炼2:△ECD≌△FAD;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
(问题解决)
(1)如图2,四边形ABCD是正方形,E为BC边上一点,连接DE,将△CDE沿DE折叠,点C落在G处,EG交AB于点F,连接DF.
可得:∠EDF= °;AF,FE,EC三者间的数量关系是 .
(2)如图3,四边形ABCD的面积为8,AB=AD,∠DAB=∠BCD=90°,连接AC.求AC的长度.
(3)如图4,在△ABC中,∠ACB=90°,CA=CB,点D,E在边AB上,∠DCE=45°.写出AD,DE,EB间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: ![]() .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法.
![]()
(1)解不等式(1),得________;
(2)解不等式(2),得________;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的不等式组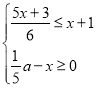 至少有3个整数解,且关于x的分式方程
至少有3个整数解,且关于x的分式方程![]() 的解为整数,则符合条件的所有整数a的取值之和为( )
的解为整数,则符合条件的所有整数a的取值之和为( )
A.﹣10B.﹣9C.﹣7D.﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
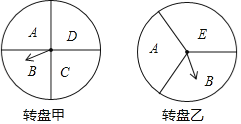
【题目】某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)若顾客选择方式一,则享受9折优惠的概率为多少;
(2)若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
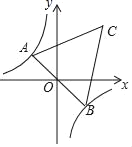
【题目】如图,在反比例函数y=-![]() 的图象上有一动点A,连结AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连结AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=![]() 的图象上运动,若tan∠CAB=3,则k的值为( )
的图象上运动,若tan∠CAB=3,则k的值为( )
A.![]() B.6C.8D.18
B.6C.8D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系xoy中,A(-4,3),反比例函数![]() 的图象分别交矩形ABOC的两边AC,BC于E,F(E,F不与A重合),沿着EF将矩形ABOC折叠使A,D重合.
的图象分别交矩形ABOC的两边AC,BC于E,F(E,F不与A重合),沿着EF将矩形ABOC折叠使A,D重合.
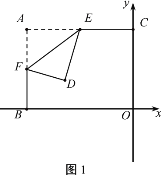
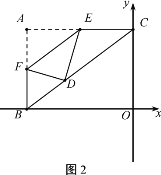
(1)①如图2,当点D恰好在矩形ABOC的对角线BC上时,求CE的长;
②若折叠后点D落在矩形ABOC内(不包括边界),求线段CE长度的取值范围.
(2)若折叠后,△ABD是等腰三角形,请直接写出此时点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com