
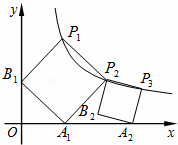
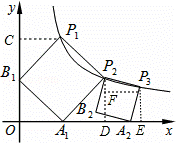
正方形的A1B1P1P2顶点P1、P2在反比例函数y=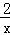 (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=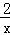 (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . .
(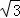 +1,
+1,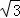 ﹣1)
﹣1)
考点: 反比例函数综合题.
专题: 综合题;压轴题.
分析: 作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,设P1(a,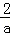 ),则CP1=a,OC=
),则CP1=a,OC=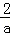 ,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D=
,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D=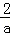 ﹣a,则P2的坐标为(
﹣a,则P2的坐标为(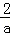 ,
,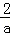 ﹣a),然后把P2的坐标代入反比例函数y=
﹣a),然后把P2的坐标代入反比例函数y=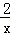 ,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b,
,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b,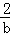 ),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE=
),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE=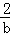 ,通过OE=OD+DE=2+
,通过OE=OD+DE=2+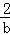 =b,这样得到关于b的方程,解方程求出b,得到P3的坐标.
=b,这样得到关于b的方程,解方程求出b,得到P3的坐标.
解答: 解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图,
设P1(a,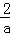 ),则CP1=a,OC=
),则CP1=a,OC=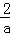 ,
,
∵四边形A1B1P1P2为正方形,
∴Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,
∴OB1=P1C=A1D=a,
∴OA1=B1C=P2D=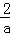 ﹣a,
﹣a,
∴OD=a+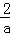 ﹣a=
﹣a=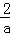 ,
,
∴P2的坐标为(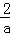 ,
,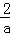 ﹣a),
﹣a),
把P2的坐标代入y=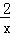 (x>0),得到(
(x>0),得到(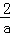 ﹣a)•
﹣a)•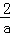 =2,解得a=﹣1(舍)或a=1,
=2,解得a=﹣1(舍)或a=1,
∴P2(2,1),
设P3的坐标为(b,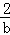 ),
),
又∵四边形P2P3A2B2为正方形,
∴Rt△P2P3F≌Rt△A2P3E,
∴P3E=P3F=DE=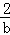 ,
,
∴OE=OD+DE=2+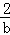 ,
,
∴2+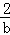 =b,解得b=1﹣
=b,解得b=1﹣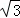 (舍),b=1+
(舍),b=1+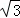 ,
,
∴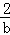 =
=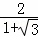 =
=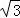 ﹣1,
﹣1,
∴点P3的坐标为 (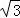 +1,
+1,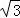 ﹣1).
﹣1).
故答案为:(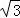 +1,
+1,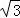 ﹣1).
﹣1).
点评: 本题考查了反比例函数图象上点的坐标特点为横纵坐标之积为定值;也考查了正方形的性质和三角形全等的判定与性质以及解分式方程的方法.


科目:初中数学 来源: 题型:
若关于x的方程x2+2ax+7a﹣10=0没有实根,那么,必有实根的方程是( )
A. x2+2ax+3a﹣2=0 B. x2+2ax+5a﹣6=0
C. x2+2ax+10a﹣21=0 D. x2+2ax+2a+3=0
查看答案和解析>>
科目:初中数学 来源: 题型:
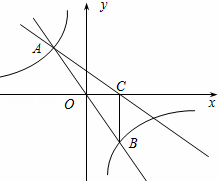
如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=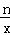 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式;
(3)结合图象直接写出当mx>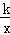 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是下面四个立体图形中的( )

A.①② B.②③ C.②③④ D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com