
若关于x的方程x2+2ax+7a﹣10=0没有实根,那么,必有实根的方程是( )
A. x2+2ax+3a﹣2=0 B. x2+2ax+5a﹣6=0
C. x2+2ax+10a﹣21=0 D. x2+2ax+2a+3=0
A
考点: 根的判别式.
专题: 计算题.
分析: 由方程x2+2ax+7a﹣10=0无实根,得到△=4a2﹣4×1×(7a﹣10)<0,即a2﹣7a+10<0,解得2<a<5;再分别计算四个选项中的方程的△,然后判断各方程根的情况.
解答: 解:∵方程x2+2ax+7a﹣10=0无实根,
∴判别式△=4a2﹣4×1×(7a﹣10)<0,即a2﹣7a+10<0,(a﹣2)(a﹣5)<0,
∴2<a<5,
四个选项中的方程的△分别为:
A、△=4(a﹣1)(a﹣2),当2<a<5,△A>0,故本选项正确;
B、△=4(a﹣2)(a﹣3),当a=2.5,△B<0,故本选项错误;
C、△=4(a﹣3)(a﹣7),当a=4,△C<0,故本选项错误;
D、△=4(a+1)(a﹣3),当a=2.5,△D=<0,故本选项错误.
故选A.
点评: 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2﹣4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了因式分解以及用它解不等式.


科目:初中数学 来源: 题型:
如图,在矩形ABCD中,E、F分别是DC、BC边上的点,且∠AEF=90°则下列结论正确的是( )
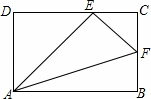
A. △ABF∽△AEF B. △ABF∽△CEF C. △CEF∽△DAE D. △DAE∽△BAF
查看答案和解析>>
科目:初中数学 来源: 题型:
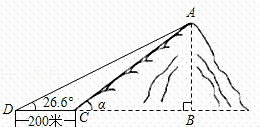
如图,小山岗的斜坡AC的坡度是tanα=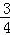 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
查看答案和解析>>
科目:初中数学 来源: 题型:
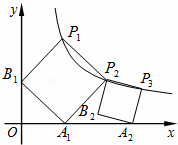
正方形的A1B1P1P2顶点P1、P2在反比例函数y=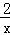 (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=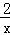 (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . .
查看答案和解析>>
科目:初中数学 来源: 题型:
某同学做数学题:已知两个多项式A、B,其中B=4x2﹣3x+7,他在求A+B时,把A+B错看成了A﹣B,求得的结果为8x2+x+1.请你帮助这位同学求出A+B的正确结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com