
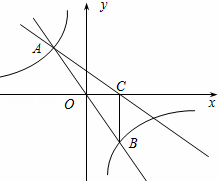
如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=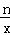 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式;
(3)结合图象直接写出当mx>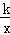 时,x的取值范围.
时,x的取值范围.
考点: 反比例函数与一次函数的交点问题.
分析: (1)由题意,根据对称性得到B的横坐标为1,确定出C的坐标,根据三角形AOC的面积求出B的纵坐标,确定出A坐标,将A坐标代入一次函数与反比例函数解析式,即可求出m与n的值;
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出直线AC的解析式.
(2)根据A、B的坐标,然后观察函数图象求解.
解答: 解:(1)∵直线y=mx与双曲线y=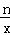 相交于A(﹣1,a)、B两点,
相交于A(﹣1,a)、B两点,
∴B(1,﹣a).
∵△BOC的面积是1,BC⊥x轴,垂足为C,
∴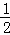 ×1×a=1,
×1×a=1,
∴a=2,
∴A(﹣1,2).
将A(﹣1,2)代入y=mx,y=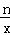 可得m=﹣2,n=﹣2;
可得m=﹣2,n=﹣2;
(2)设直线AC的解析式为y=kx+b,
∵y=kx+b经过点A(﹣1,2)、C(1,0)
∴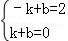 ,
,
解得k=﹣1,b=1,
∴直线AC的解析式为y=﹣x+1.
(3)由图象可知:当mx> 时,x<﹣1或0<x<1.
时,x<﹣1或0<x<1.
点评: 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:反比例函数的图象与性质,待定系数法确定函数解析式,熟练掌握待定系数法是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
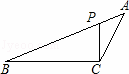
如图,在△ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC与△ACB相似的条件是 (只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
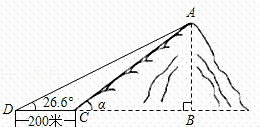
如图,小山岗的斜坡AC的坡度是tanα=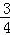 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
查看答案和解析>>
科目:初中数学 来源: 题型:
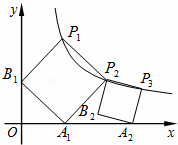
正方形的A1B1P1P2顶点P1、P2在反比例函数y=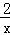 (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=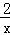 (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . .
查看答案和解析>>
科目:初中数学 来源: 题型:
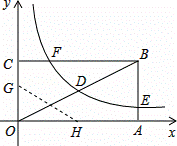
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=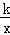 (k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.
(k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com