练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．边长都为整数的△ABC和△DEF全等，AB与DE是对应边，AB=2，BC=4，若△DEF的周长为奇数，则DF的值为（　　）
    A．3B．4C．3或5D．3或4或5

    分析 根据三角形的三边关系求得AC的范围，然后根据全等三角形的对应边相等即可求解．

    解答 解：AC的范围是2＜AC＜6，则AC的奇数值是3或5．
    △ABC和△DEF全等，AB与DE是对应边，则DE=AB=2，
    当DF=AC时，DF=3或5．
    当DF=BC时，DF=4．
    故选D．

    点评 本题考查了三角形的三边关系以及全等三角形的性质，正确对三角形进行讨论是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．已知：如图，在△ABC中，∠C=90°，AE平分∠CAB，且BE2=DE•AE．求证：BE⊥AE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

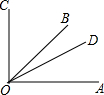    10．如图，已知∠COA=90°，∠COD比∠DOA大n°，且OB是∠COA的平分线．
    （1）若n=36，求∠BOD的度数；
    （2）直接用n的式子表示∠BOD为$\frac{1}{2}$n度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，已知AB=6，C为AB的一个四等分点，D为BC的中点，则AD=（　　）
    A．$\frac{15}{4}$B．$\frac{15}{2}$C．4D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

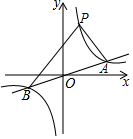    14．如图，反比例函数y=$\frac{k}{x}$与y=mx交于A、B两点，已知点A的坐标是（4，2），点P是第一象限内反比例函数图象上的动点，且在AB的上方．
    （1）求k、m的值，写出B点的坐标；
    （2）在x轴上有一点Q，使△ABQ为等腰三角形，写出点Q的坐标，并说明为什么？
    （3）若S△ABP=12，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：如果|a-1|+|ab-2|=0．求$\frac{1}{ab}$+$\frac{1}{（a+1）（b+1）}$+$\frac{1}{（a+2）（b+2）}$+…+$\frac{1}{（a+2013）（b+2013）}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知△ABC的三边满足a2-2bc-c2+2ab=0，判断△ABC的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

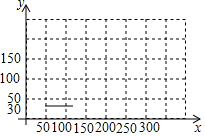    8．某电信公司提供的移动通讯服务的收费标准有两种方案，如表所示：
    A方案B方案
    每月基本服务费30元50元
    每月免费通话时间120分200分
    超出后每分钟收费0.4元0.4元
    设每月通话时间为x分，A，B两种方案每月话费分别为y1元，y2元．
    （1）分别写出当x＞120时，y1关于x的函数表达式和当x＞200时，y2关于x的函数表达式；
    （2）在如图所示的平面直角坐标系中，把y1和y2这两个函数图象的其余部分补画出来；（实线为A方案，虚线为B方案）
    （3）结合图象考虑，若以节省费用的角度考虑，则应如何选择最优方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，点E，F在BC上，BE=CF，∠AFE=∠DEF，∠B=∠C，求证：AB=DC．

    查看答案和解析>>

    同步练习册答案